ハノイの塔:パズルの魅力と奥深さ

AIを知りたい
先生、「ハノイの塔」ってパズルは知っていますが、AIと何か関係があるのですか?

AIエンジニア
良い質問ですね。ハノイの塔は、AIの分野、特に「探索アルゴリズム」の学習に役立つ教材なんです。

AIを知りたい
探索アルゴリズム…ですか?

AIエンジニア
そうです。AIは、どのように円盤を動かせば目的の状態にたどり着けるかを、ハノイの塔を通して学ぶことができます。これは、問題解決の手順を学ぶ上で最適な例なんです。AIが様々な問題を解くための手順を学ぶのに、ハノイの塔のような問題はうってつけなのです。
ハノイの塔とは。
知能を持った機械に関係する言葉、『ハノイの塔』について説明します。ハノイの塔は、考え方を試す遊びです。三本の棒と、大きさが違い、真ん中に穴の開いた円盤がいくつかあります。はじめは、左側の棒に、大きい円盤が下になるように重ねられています。一回ごとに、円盤を別の棒に動かすことができます。ただし、大きい円盤を小さい円盤の上に重ねてはいけません。全ての円盤を右側の棒に移動させることができたら終わりです。終わりまでに必要な回数は計算で求めることができ、円盤の枚数をnとすると、二のn乗から一を引いた回数になります。
歴史と概要

「ハノイの塔」は、フランスの数学者エドゥアール・リュカが1883年に作った、世界的に有名なパズルです。このパズルは、3本の棒と、真ん中に穴のあいた大きさの違う円盤でできています。円盤には大小様々なものがあり、遊ぶ人が自由に枚数を選べます。
遊び方は、まず全ての円盤を左端の棒に、大きい円盤ほど下にくるように重ねて並べます。そして、これらの円盤を全て右端の棒に、同じ順番で移すことが目的です。円盤を動かすときには、必ず3本の棒のいずれかを使わなければなりません。また、一度に動かせる円盤は1枚だけで、小さい円盤の上に大きい円盤を重ねて置いてはいけません。
一見すると簡単なルールのように思えますが、円盤の枚数が増えると、解くための手順は驚くほど複雑になります。例えば、円盤が3枚の場合、最短でも7回の移動が必要です。4枚だと15回、5枚だと31回と、枚数が増えるごとに必要な手数は急激に増えていきます。リュカは、このパズルを「ルーカス・タワー」と名付け、ベトナムのハノイにある寺院にまつわる伝説を創作して、その神秘性を高めました。実際には、ハノイの寺院との関連性は薄いとされていますが、この伝説によって「ハノイの塔」という名前が広く知られるようになりました。
ハノイの塔は、数学や情報科学の分野で、アルゴリズムや再帰的思考を学ぶための教材としても活用されています。シンプルなルールでありながら、奥深い論理的思考が求められるパズルとして、世界中の人々に楽しまれています。
| 項目 | 内容 |
|---|---|
| 名称 | ハノイの塔 |
| 考案者 | エドゥアール・リュカ (フランスの数学者) |
| 考案年 | 1883年 |
| 内容物 | 3本の棒、中央に穴の空いた大きさの異なる円盤 |
| ルール |
|
| 難易度 | 円盤の枚数が増えるごとに指数関数的に増加 |
| 例 | 3枚:7回、4枚:15回、5枚:31回 |
| 別名 | ルーカス・タワー |
| 伝説 | ベトナムのハノイにある寺院にまつわる伝説(実際には関連性薄) |
| 活用 | 数学や情報科学の分野で、アルゴリズムや再帰的思考を学ぶための教材 |
解法の考え方

ハノイの塔という、知恵の輪をご存じでしょうか。これは、大きさの異なる円盤が積み重なった塔を、別の棒へ移動させるパズルです。ルールはシンプルで、一度に一枚の円盤しか動かせず、小さい円盤の上に大きい円盤を置くことはできません。一見簡単そうですが、円盤の枚数が増えると、途端に複雑になります。
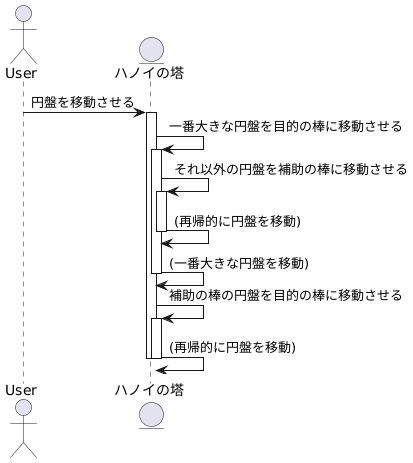
このパズルを解くための鍵となるのが、再帰的という考え方です。これは、問題をより小さな同じ種類の問題に分解して解決していく手法です。ハノイの塔の場合、円盤が何枚あっても、最終的には一番大きな円盤を目的の棒に移動させることが目標となります。そこで、まずは一番大きな円盤を移動させるために、それ以外の円盤を補助の棒に移動させるという、小さな問題に分解します。
具体的に見てみましょう。三枚の円盤がある場合、まず上の二枚を補助の棒に移動させます。次に、一番大きな円盤を目的の棒に移動させます。そして最後に、補助の棒にある二枚の円盤を目的の棒に移動させます。ここで重要なのは、二枚の円盤を移動させる手順も、同じ考え方でさらに分解できるということです。つまり、まず一番上の円盤を空いている棒に移動し、次に二番目の円盤を目的の棒に移動し、最後に空いている棒にある円盤を目的の棒に移動させます。
このように、問題を小さな同じ種類の問題に分解し、それを繰り返すことで、最終的にすべての円盤を目的の棒に移動させることができます。この再帰的な考え方は、ハノイの塔だけでなく、様々な問題解決に応用できる、強力な手法と言えるでしょう。
最小移動回数

ハノイの塔という、杭と積み重ねられた円盤を移動させるパズルがあります。このパズルは、決められたルールに従ってすべての円盤を別の杭に移動させることを目的としています。ルールはシンプルですが、円盤の枚数が増えると、パズルを解くのは難しくなります。いったい、最短で何回移動すれば解けるのでしょうか。
実は、最小の移動回数は、円盤の枚数によって決まっています。円盤の枚数を「n」とすると、最小移動回数は「2のn乗 から1を引いた数」で計算できます。例えば、円盤が3枚ある場合は、2の3乗は8なので、そこから1を引いた7回が最小の移動回数となります。同様に、円盤が4枚の場合は、2の4乗は16なので、そこから1を引いた15回が最小の移動回数です。
このように、円盤の枚数が1枚増えるごとに、最小移動回数はほぼ2倍になります。これを指数関数的な増加と言います。つまり、円盤の枚数が少し増えるだけでも、最小移動回数は急激に増えていくのです。そのため、円盤の枚数が多くなると、実際にパズルを解くのはとても大変になります。5枚の円盤だと31回、6枚だと63回と、想像以上に移動回数が増えていきます。
この最小移動回数は、ハノイの塔の難しさを示す目安となります。また、コンピュータでこのパズルを解くプログラムを作る際の、効率の良さを評価する指標としても使われます。
| 円盤の枚数(n) | 最小移動回数 (2n – 1) |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 7 |
| 4 | 15 |
| 5 | 31 |
| 6 | 63 |
遊び方と学び

ハノイの塔は、楽しみながら知的な力を伸ばせる、優れた教材です。遊びを通して論理的思考力や問題解決能力を高められるだけでなく、情報処理の基礎となる考え方にも触れられます。
具体的な遊び方としては、まず木の棒三本と大きさの異なる円盤を用意します。目標は、積み重なった円盤を別の棒に、同じ順番で移動させることです。ただし、一度に動かせる円盤は一枚だけで、小さい円盤の上に大きい円盤を置くことはできません。このルールを守りながら、どうすれば効率的に移動できるかを考えることが、この遊びの核心です。
実際に円盤と棒を使って遊ぶことで、試行錯誤しながら解法を探る喜びを味わえます。円盤の枚数を増やすごとに難易度が上がり、より深い思考が必要になります。また、計算機上で模擬実験をすることも可能です。画面上で円盤を動かしながら、様々な手順を試すことができます。
ハノイの塔には、最小移動回数を求める公式が存在します。この公式を学ぶことで、数学的な見方も養えます。円盤の枚数と移動回数の関係を分析し、公式の背後にある数学的な原理を探るのも、学びを深める良い方法です。さらに、計算機に指示を与える手順を書き出すことで、情報処理の基礎を学ぶこともできます。円盤の動かし方を順序立てて考えることは、まさに手順を組み立てる練習です。
このように、ハノイの塔は、遊びと学びを両立できる、教育的に価値のあるパズルです。楽しみながら考える力を伸ばし、将来役立つ基礎を築くことができるでしょう。
| 項目 | 説明 |
|---|---|
| 概要 | 楽しみながら知的な力を伸ばせる優れた教材。論理的思考力、問題解決能力、情報処理の基礎となる考え方を養える。 |
| 遊び方 | 大きさの異なる円盤を、ルールに従って別の棒に移動させる。小さい円盤の上に大きい円盤を置くことはできない。 |
| 学習効果 | 試行錯誤、難易度調整、数学的見方、情報処理の基礎を学べる。 |
| 数学的側面 | 最小移動回数を求める公式が存在し、数学的原理の探求が可能。 |
| 情報処理的側面 | 円盤の動かし方を順序立てて考えることで、手順を組み立てる練習になる。 |
様々な応用

ハノイの塔は、一見単純な遊び道具のように見えますが、実は様々な分野で活用されています。その活用範囲は、遊びの枠を超えて、学問の世界にまで広がっています。
まず、人の心の働きを調べる学問である心理学の分野では、ハノイの塔は、人がどのように考え、問題を解決していくのかを調べるための道具として使われています。ハノイの塔を解く様子を観察することで、思考力や判断力といった、人それぞれの考え方の特徴を捉えることができると考えられています。
次に、計算機を扱う学問である情報科学の分野では、計算の手順を効率よく行うための方法を研究する際に、ハノイの塔が役立っています。これは、ハノイの塔を解く手順が、計算の手順とよく似ているためです。ハノイの塔を使って、様々な計算方法を試すことで、より速く、より正確な計算方法を見つけることができます。
さらに、物事の戦略を考える学問であるゲーム理論や、人の知能を機械で再現しようとする人工知能の研究にも、ハノイの塔は応用されています。複雑な問題を解決するための手順を考える上で、ハノイの塔は、格好の例題となっているのです。
このように、ハノイの塔は、一見単純な遊びに見えますが、人の心の働きや計算の手順、戦略の組み立てといった、様々な学問分野と深く関わっていることが分かります。このことから、ハノイの塔は、学術的にも重要なパズルとして、高く評価されています。
| 活用分野 | 活用目的 |
|---|---|
| 心理学 | 思考力や判断力など、人それぞれの考え方の特徴を捉える |
| 情報科学 | 計算の手順を効率よく行うための方法を研究 |
| ゲーム理論、人工知能 | 複雑な問題を解決するための手順を考える上での例題 |
パズルの魅力

{頭をひねって考え抜く楽しさ}、これがパズルの最大の魅力です。たとえば、ハノイの塔というパズルを考えてみましょう。このパズルは、とても簡単な決まり事と、思いもよらないほどの奥深さを併せ持っています。遊び方はとても単純で、誰でもすぐに理解し、遊び始めることができます。しかし、円盤の枚数を少し増やすだけで、解き方は驚くほど複雑になります。
少ない手数で解こうと試行錯誤するうちに、自然と論理的に考える力や、問題を解決する力が鍛えられます。パズルを解くには、まず全体像を把握し、どのように円盤を動かせば目的の状態に近づけるかを考えなければなりません。そして、一つずつ手順を確認しながら、慎重に円盤を動かしていく必要があります。行き詰まった時には、これまで試した方法を振り返り、別のやり方を考える柔軟さも求められます。
ハノイの塔には「最短の手数」という明確な目標があります。この目標があるからこそ、より効率的な解き方を追求しようという意欲が湧いてきます。どうすれば無駄な手順を省けるのか、どうすれば最短の手数で解けるのか、試行錯誤を繰り返すうちに、思考力はさらに研ぎ澄まされていくでしょう。
このように、簡単なルールの中に、やりがいのある難しさが隠されていることが、ハノイの塔が長年多くの人々に愛され続けている理由の一つと言えるでしょう。多くのパズルは、ハノイの塔のように、単純なルールと奥深い思考のバランスが取れているからこそ、世代を超えて楽しまれているのです。夢中になってパズルに取り組むうちに、知らず知らずのうちに思考力が鍛えられている、それがパズルの魅力と言えるでしょう。
| 項目 | 説明 |
|---|---|
| パズルの魅力 | 頭をひねって考え抜く楽しさ |
| ハノイの塔の特徴 |
|
| ハノイの塔で鍛えられる力 |
|
| ハノイの塔の目標 | 最短の手数で解く |
| ハノイの塔が愛される理由 | 簡単なルールの中にやりがいのある難しさが隠されている |
| 多くのパズルが世代を超えて楽しまれる理由 | 単純なルールと奥深い思考のバランスが取れている |
