つながりの数学:グラフ理論の世界

AIを知りたい
先生、「グラフ理論」って、電車の路線図のように、駅と駅が線でつながっている様子を表すものですよね?

AIエンジニア
そうだね。路線図は良い例えだ。グラフ理論では、駅のような「点」と、路線のような「線」の関係性を数学的に考えていくんだよ。

AIを知りたい
じゃあ、点と線がつながっている様子なら何でもグラフ理論で考えられるんですか?

AIエンジニア
そうとも言えるね。例えば、友達同士の関係やインターネットのネットワーク構造なんかもグラフ理論で考えることができる。大切なのは「つながり方」に着目することなんだよ。
グラフ理論とは。
人と人、ものともの、場所と場所など、様々なものがどのようにつながっているかを数学的に調べる学問である「グラフ理論」について説明します。この学問は、1736年にオイラーという数学者が、ケーニヒスベルクという町の橋をすべて一度だけ渡って元の場所に戻れるかという問題を解いたことがきっかけの一つとして始まりました。最近では、このグラフ理論が、企業活動など現実の問題を解決するのに役立つと注目されています。というのも、グラフ理論を使うと複雑な関係性を簡単に表すことができ、さらに計算機の学習方法が進歩したことで、これまで以上に色々な分析ができるようになったからです。グラフ理論にはたくさんの使い道がありますが、中でもよく知られているのが、都市間の最短経路を見つけるというものです。例えば、電車の路線図を思い浮かべてみてください。路線図では、駅と駅がどのように線でつながっているかが重要で、駅と駅の間の実際の距離や位置関係、路線の形などはあまり気にしません。路線図を使う人にとって大切なのは、どの駅とどの駅がつながっているかということだからです。このように、ものごとのつながり方に注目して、点と線で単純に表したものを「グラフ」といい、グラフの持つ様々な性質を調べるのがグラフ理論です。
起源と歴史

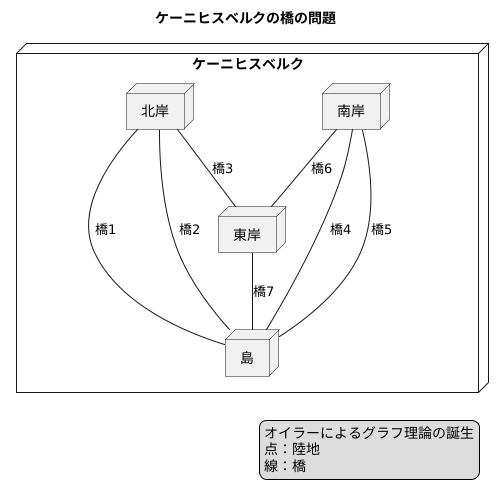
18世紀のヨーロッパ、プロイセン王国のケーニヒスベルクという街にプレゲリャ川という川が流れていました。街の中央には島があり、7つの橋が架けられていました。当時、この街の人々の間で、ある疑問が話題になっていました。『すべての橋を一度だけ渡り、元の場所に戻ってくることができるか?』という問題です。日曜日の散歩の度に、人々はこの難問に挑戦していましたが、誰一人として成功しませんでした。
この一見単純そうな問題は、多くの数学者たちの関心を集めました。誰もが解法を見つけようとしましたが、皆、失敗に終わりました。そんな中、スイスの数学者レオンハルト・オイラーがこの問題に挑戦しました。オイラーは、この問題を解くために、画期的な方法を思いつきました。それは、陸地を点、橋を線で表すという方法です。現在ではグラフと呼ばれるこの表現方法を用いることで、オイラーは問題を単純化することに成功しました。そして、すべての橋を一度だけ渡って元の場所に戻ることは不可能であることを、数学的に証明しました。1736年に発表されたオイラーの論文は、グラフ理論の誕生を告げるものでした。それまで、図形を扱う幾何学では、線の長さや角度といった量的な性質が重要視されていました。しかし、オイラーは、線の長さや角度を無視し、点と線の繋がり方という、質的な性質に着目することで、新たな数学の分野を切り開いたのです。
こうして生まれたグラフ理論は、その後、数多くの数学者たちによって研究され、発展を遂げてきました。現代社会においても、インターネットのネットワーク構造の解析や、交通網の最適化、人工知能の開発など、様々な分野で応用されています。ケーニヒスベルクの橋の問題は、単なる頭の体操ではなく、現代社会の様々な問題を解決する強力な道具となる学問分野の出発点だったのです。
グラフ理論とは何か

ものの繋がり方を点と線で表し、その特徴を調べる数学の一分野が、グラフ理論と呼ばれています。ここで、点は「頂点」、線は「辺」と言い表します。
身近な例で説明すると、電車の路線図が分かりやすいでしょう。駅一つ一つが頂点であり、駅と駅をつなぐ路線が辺にあたります。路線図を見ると、駅と駅の距離や、駅の正確な場所は分かりません。路線図が私たちに教えてくれるのは、どの駅とどの駅が繋がっているか、つまり駅同士の繋がり方だけです。グラフ理論もこれと同じように、ものごとの繋がり方に注目します。
ものごとの関係性は、複雑で分かりにくい場合が多いです。そこで、複雑な関係性を単純な図形に置き換えることで、ものごとの本質を捉えようとするのがグラフ理論の考え方です。
例えば、友達関係をグラフ理論で表すこともできます。この場合、一人一人が頂点になり、友達同士であれば頂点と頂点の間に辺を引きます。こうして図示してみると、誰が誰と友達で、どのグループの人数が多く、誰が中心的な人物なのかといったことが、視覚的に分かりやすくなります。
このように、一見単純な点と線による表現方法ですが、複雑な問題を解き明かす強力な道具となるのです。例えば、カーナビゲーションシステムでの最短経路探索、インターネットでの情報伝達、ソーシャルネットワークの分析など、グラフ理論は様々な分野で応用され、私たちの生活を支えています。
| 用語 | 説明 | 例 |
|---|---|---|
| グラフ理論 | ものの繋がり方を点と線で表し、その特徴を調べる数学の一分野 | 電車の路線図、友達関係、カーナビゲーションシステム、インターネット、ソーシャルネットワークなど |
| 頂点 | 点のこと | 駅、人 |
| 辺 | 線のこと。頂点と頂点を繋ぐ。 | 路線、友達関係 |
グラフ理論の応用例

グラフ理論は、目に見えない繋がりを視覚的に捉え、分析するための強力な道具です。私たちの日常生活から最先端技術まで、様々な場面で応用されています。
例えば、カーナビゲーションシステムを考えてみましょう。カーナビは、道路網をグラフとして表現しています。交差点がグラフの「点」であり、道路が「線」に当たります。点と線で構成された道路網をグラフとして捉えることで、出発地から目的地までの最短経路を計算することができます。さらに、道路の混雑状況や通行止め情報などもグラフに反映することで、より正確で効率的な経路案内が可能になります。
インターネットもまた、グラフ理論の応用が欠かせない分野です。世界中に広がるコンピュータネットワークは、巨大なグラフとして表現できます。それぞれのコンピュータが「点」であり、それらを繋ぐ通信回線が「線」です。情報を効率的に伝達するためには、最適な経路設計が不可欠です。グラフ理論を用いることで、データの送受信をスムーズに行うための経路を見つけ、ネットワーク全体の性能を向上させることができます。また、一部の回線が故障した場合でも、代替経路を迅速に見つけることで、ネットワークの安定性を維持することができます。
人間関係の分析にもグラフ理論は役立ちます。例えば、交流サイト(SNS)では、利用者一人ひとりを「点」とし、繋がりを「線」とすることで、人々の関係性をグラフで表すことができます。このグラフを分析することで、情報の伝わり方や影響力のある人物を特定することができます。企業は、新商品の宣伝戦略を立てる際などに、これらの情報を活用しています。
このように、グラフ理論は、現代社会の様々な場面で問題解決に役立つ重要な道具となっています。今後、さらに技術が発展していくにつれて、グラフ理論の応用範囲はますます広がっていくことでしょう。
| 分野 | 点 | 線 | グラフ理論の活用例 |
|---|---|---|---|
| カーナビゲーション | 交差点 | 道路 | 最短経路計算、道路状況に応じた経路案内 |
| インターネット | コンピュータ | 通信回線 | 効率的な情報伝達、代替経路の確保 |
| 人間関係分析(SNS) | 利用者 | 繋がり | 情報の伝播分析、影響力のある人物特定 |
最短経路問題

道順を探す問題は、暮らしの中でとても身近なものです。例えば、お店への行き方や、友達の家への道順など、日々無意識に最短の道を探しています。これをコンピュータで解くのが、最短経路問題です。
最短経路問題は、「グラフ」と呼ばれる繋がりを表現したものを使って考えます。グラフは、いくつかの点と、それらを結ぶ線でできています。点を「頂点」、線を「辺」と呼びます。例えば、地図上で都市を頂点、都市間の道路を辺と考えると、地図全体が一つのグラフとして表せます。道の長さを辺に書き込むことで、都市間の距離が分かります。
最短経路問題とは、このグラフ上で、ある頂点から別の頂点へ行く最短の道を見つける問題です。 例えば、カーナビゲーションシステムは、出発地と目的地を入力すると、道路網をグラフとして捉え、最短経路を計算して画面に表示します。このとき、道路の混雑状況や通行止め情報なども考慮することで、より現実に即した最短経路を計算できます。
最短経路問題を解くための方法はいくつかあります。例えば、「ダイクストラ法」は、ある頂点から他の全ての頂点への最短経路を計算する効率的な方法です。また、「ベルマン-フォード法」は、辺の長さが負の場合にも適用できる方法です。他にも、様々な方法が研究されており、問題の性質や条件に応じて使い分けられます。
最短経路問題は、カーナビゲーション以外にも、様々な場面で活用されています。例えば、物流会社では、配送トラックの最適なルートを決定するために最短経路問題を利用しています。また、災害時には、避難所までの最短経路を計算することで、迅速な避難誘導が可能になります。インターネットの通信経路の最適化にも、最短経路問題の考え方が応用されています。このように、最短経路問題は、私たちの生活を支える様々なシステムで重要な役割を果たしています。
| 概念 | 説明 | 例 |
|---|---|---|
| 最短経路問題 | グラフ上で、ある頂点から別の頂点へ行く最短の道を見つける問題 | カーナビゲーション、物流ルート最適化、避難経路探索、インターネット通信経路最適化 |
| グラフ | 繋がりを表現するもの。頂点と辺で構成される。 | 地図:都市(頂点), 道路(辺) |
| 頂点 | グラフを構成する点 | 都市 |
| 辺 | グラフを構成する線。頂点同士を結ぶ。 | 道路 |
| ダイクストラ法 | ある頂点から他の全ての頂点への最短経路を計算する効率的な方法 | – |
| ベルマン-フォード法 | 辺の長さが負の場合にも適用できる方法 | – |
機械学習との関連

近年、繋がりを表現する数学的手法であるグラフ理論が、機械学習の分野で大きな注目を集めています。機械学習とは、計算機に大量の情報を学習させ、未知の情報に対しても予測や判断を可能にする技術です。この機械学習の中でも、特にグラフ構造を持つ情報を扱う手法として、「グラフニューラルネットワーク(グラフ神経回路網)」、略して「グラフ神経網」が期待されています。
グラフ神経網は、繋がりの情報を効果的に学習できる点が大きな特徴です。例えば、分子の構造は原子同士の繋がりで表現できます。この繋がり方をグラフ神経網に学習させることで、新しい分子の性質や機能を予測することが可能になります。また、人の繋がりを表現した「繋がり合う仲間の集まり」の分析にもグラフ神経網は役立ちます。どの仲間と誰が繋がっているかという情報を基に、集団全体の傾向や個人の役割を分析することができます。
さらに、インターネット上の買い物でよく見かける「おすすめ機能」にも、グラフ神経網は活用されています。誰がどの商品を購入したか、どの商品とどの商品が一緒に購入されることが多いか、といった情報をグラフ構造として捉え、個々の利用者におすすめの商品を提示することができます。このように、グラフ神経網は様々な分野で応用されており、その可能性は広がり続けています。
グラフ理論と機械学習の組み合わせは、今後ますます発展していくと考えられています。新しい理論や技術の開発によって、これまで解決できなかった問題が解決できるようになる可能性も秘めています。例えば、創薬の分野では、より効果の高い薬の開発に繋がるかもしれませんし、複雑な社会現象の解明にも役立つかもしれません。グラフ理論と機械学習の融合は、様々な分野で革新をもたらす力を持っており、今後の発展に大きな期待が寄せられています。
| 分野 | 活用例 | 説明 |
|---|---|---|
| 化学 | 分子の性質・機能予測 | 原子同士の繋がりを学習し、新しい分子の性質や機能を予測 |
| 社会科学 | 繋がり合う仲間の集まりの分析 | 誰が誰と繋がっているかを分析し、集団全体の傾向や個人の役割を分析 |
| 情報科学 | おすすめ機能 | 購入履歴や商品間の関連性をグラフ構造として捉え、個々の利用者におすすめ商品を提示 |
今後の展望

繋がりを図に表す考え方は、様々な分野で今後ますます使われていく見込みです。特に、近頃は多くの情報が集まるようになってきており、複雑に絡み合った物事の関係を分かりやすく捉え、調べたり整理したりする道具として、この考え方はますます大切になっています。人工知能の成長や、集まった大量の情報の分析、人と人、あるいは物と物がどのように繋がっているかを研究するネットワーク科学など、多くの分野と結びつくことで、この繋がりを図に表す考え方はさらに進化し、私たちの暮らしに大きな変化をもたらすでしょう。
これからの研究では、図の繋がりを調べる新しい計算方法や分析方法が見つかり、今よりももっと複雑な問題を解けるようになると期待されています。例えば、人々の繋がりの変化を予測することで、流行の発生を事前に察知したり、病気の広がりを抑え込んだりすることができるかもしれません。また、商品の売れ行きを予測することで、企業はより効率的な生産計画を立てることができるようになるでしょう。
さらに、繋がりを図に表す考え方を学ぶ人が増えれば、もっと多くの分野でこの考え方が活用され、社会の進歩に役立つでしょう。例えば、都市計画においては、交通網の最適化や災害時の避難経路の設計に役立ちます。また、医療分野では、病気の伝染経路の解析や新薬開発に繋がることが期待されます。教育分野では、生徒同士の学習ネットワークを分析することで、より効果的な学習方法の開発に役立てることができます。このように、様々な分野で活用されることで、私たちの社会はより便利で安全なものになっていくでしょう。これらの発展には、多くの人々が繋がりを図に表す考え方を理解し、活用していくことが重要です。