最長距離法:データの分類手法

AIを知りたい
先生、『最長距離法』って、どういうものですか?

AIエンジニア
簡単に言うと、たくさんのデータが集まった塊をいくつか作る時のやり方の一つだよ。それぞれの塊の中のデータ同士の距離で一番遠いものを、塊と塊の間の距離として使うんだ。

AIを知りたい
塊の中のデータで一番遠い距離を使うっていうのは、どういうことですか?

AIエンジニア
例えば、A、B、Cの3つのデータで塊を作るとする。AとBの距離が1、AとCの距離が3、BとCの距離が5だとすると、BとCの距離が一番遠い5だよね?だから、この塊と他の塊との距離は5と考えるんだよ。他の塊との距離を測る時も、それぞれの塊の中で一番遠いデータ同士の距離を使うんだ。
最長距離法とは。
人工知能の分野で出てくる『最長距離法』について説明します。これは『最短距離法』とは反対の考え方で計算するやり方で、『完全連結法』とも呼ばれます。いくつかのものの集まり(これをクラスタと呼びます)を比べていく際に、それぞれの集まりに属するすべてのものの間の距離を測り、その中で一番遠い距離を、集まりと集まりの間の距離とみなす方法です。
手法の仕組み

ものの集まりをいくつかのまとまりに分ける方法の一つに、最長距離法というものがあります。この方法は、まとまり同士の間の離れ具合を測る時に、それぞれのまとまりに含まれるもの同士の離れ具合で一番遠いものを基準にするのが特徴です。
たとえば、二つのまとまりを考えてみましょう。それぞれのまとまりにはたくさんのものが含まれています。これらのまとまり同士の離れ具合を測るには、まず、片方のまとまりに含まれるすべてのものと、もう片方のまとまりに含まれるすべてのものとの間の離れ具合を一つずつ測っていきます。そして、これらの測った値の中で一番大きい値を、二つのまとまり間の離れ具合として採用するのです。
もう少し詳しく説明すると、それぞれのまとまりは、まるで小さな島のようで、島の中にたくさんの家が建っていると想像してみてください。それぞれの家は、データを表しています。そして、家と家の間の距離は、データ間の類似度や非類似度を表しています。二つの島の距離を測るということは、二つのまとまりがどれくらい似ているか、あるいは異なっているかを測るということです。最長距離法では、二つの島にある家の中から、最も遠い家同士の距離を測り、その距離を二つの島の距離とするのです。
このように、最長距離法は、最も遠いもの同士の距離を基準にすることで、まとまり同士が大きく異なるように分類する方法です。この方法は、まとまりの中に含まれるもののばらつきを抑え、それぞれのまとまりをより明確に区別したい場合に有効です。一方で、極端な値に影響されやすいという欠点もあります。例えば、あるまとまりに一つだけ他のものから大きく離れたものがあると、その一つのものの影響で、まとまり同士の距離が大きく見積もられてしまう可能性があります。
完全連結法との関係

最長距離法は、完全連結法とも呼ばれています。この二つの呼び方は、同じ手法を指す異なる表現です。なぜ「完全連結法」と呼ばれるのかというと、この手法は、異なる集団(クラスタ)間の距離を測る際に、集団に属する全てのデータ間の距離を一つ残らず考慮に入れるからです。
具体的に説明すると、二つの集団があったとします。それぞれの集団には複数のデータが含まれています。最長距離法では、まず、第一の集団に属するデータと、第二の集団に属するデータの間の距離を、全ての組み合わせについて計算します。つまり、第一の集団のデータAと第二の集団のデータB、第一の集団のデータAと第二の集団のデータC、第一の集団のデータBと第二の集団のデータB…といった具合に、考えられる限りのデータのペアについて、その間の距離を求めます。
そして、こうして計算された距離の中で、最も大きい値が、二つの集団間の距離として採用されます。このことから、「最も遠い距離」を測る方法、という意味で「最長距離法」と呼ばれます。同時に、集団内の全てのデータ間の繋がりを考慮に入れている、という意味で「完全連結法」とも呼ばれるのです。
このように、最長距離法(完全連結法)は、集団間の距離を測る際に、最悪のケースを想定していると言えます。最も遠いデータ間の距離を基準とすることで、二つの集団がどれほど離れているかをより慎重に評価しているのです。これは、データの分析において、より保守的な結果を得たい場合に有効な手法と言えるでしょう。
| 手法名 | 別名 | 距離の測り方 | 特徴 |
|---|---|---|---|
| 最長距離法 | 完全連結法 | 二つの集団に属するデータ間の全ての組み合わせの距離を計算し、その最大値を採用 |
|
最短距離法との違い

二つのものをまとめるやり方の一つに、対象同士の間の隔たりを測る方法があります。この方法には、様々な種類がありますが、ここでは『一番遠いもの同士の隔たり』を使うやり方と、『一番近いもの同士の隔たり』を使うやり方の違いについて説明します。
『一番遠いもの同士の隔たり』を使うやり方は、二つの集団それぞれに属するもの同士の隔たりのうち、最も遠い隔たりを用いて集団間の隔たりとします。例えば、東京のグループと大阪のグループをまとめる際に、東京グループの北端に住む人と大阪グループの南端に住む人の間の隔たりを用いるということです。このやり方は、一つでも飛び抜けて遠いものがあると、それに大きく影響を受けるという特徴があります。そのため、結果として小さくまとまった集団ができやすいです。
一方、『一番近いもの同士の隔たり』を使うやり方は、二つの集団それぞれに属するもの同士の隔たりのうち、最も近い隔たりを用いて集団間の隔たりとします。先ほどの例で言えば、東京グループの西端に住む人と大阪グループの東端に住む人の間の隔たりを用いるということです。このやり方は、極端に遠いものが存在していても、影響を受けにくいという特徴があります。その反面、鎖のように細長く連なった集団ができやすいという性質も持っています。
このように、隔たりの測り方の違いによって、最終的に出来上がる集団の形が大きく変わる可能性があります。同じデータを使っていても、これらのやり方では異なる結果が得られる場合があるので、分析の目的やデータの性質に合わせて適切な方法を選ぶことが重要です。
| 項目 | 一番遠いもの同士の隔たり | 一番近いもの同士の隔たり |
|---|---|---|
| 集団間の隔たりの定義 | 二つの集団それぞれに属するもの同士の隔たりのうち、最も遠い隔たり | 二つの集団それぞれに属するもの同士の隔たりのうち、最も近い隔たり |
| 例 | 東京グループの北端の人と大阪グループの南端の人の間の隔たり | 東京グループの西端の人と大阪グループの東端の人の間の隔たり |
| 特徴 | 飛び抜けて遠いものに大きく影響を受ける。小さくまとまった集団ができやすい。 | 極端に遠いものの影響を受けにくい。鎖のように細長く連なった集団ができやすい。 |
計算の手順

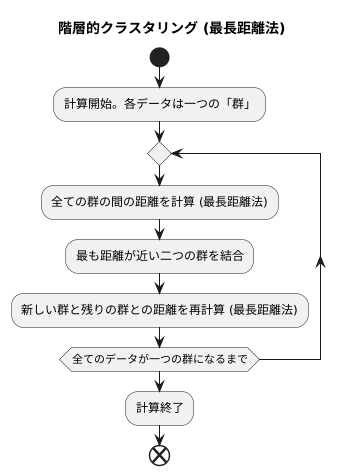
計算を始めるときには、全てのデータをそれぞれ独立した小さな集団として扱います。言いかえると、データ一つ一つが、それぞれ一つの集団になっている状態です。この小さな集団のことを、ここでは「群」と呼ぶことにします。
次に、それぞれの群の間の距離を測ります。距離の測り方にはいくつかありますが、ここでは群に属するデータ同士の距離の中で、最も遠い距離をその群同士の距離として採用します。この方法を最長距離法と呼びます。
全ての群の間の距離が測れたら、最も距離が近い二つの群を一つにまとめ、新たな群を作ります。そして、新しくできた群と、残りの群との間の距離をもう一度計算し直します。この時にも、最長距離法を用いて距離を測ります。
このように、群同士の距離を測り、近い群をまとめていくという手順を繰り返します。すると、最終的には全てのデータが一つの大きな群にまとまります。これが計算の終わりです。
群同士の距離を一覧にした表を用いると、計算がしやすくなります。この表は、どの群とどの群がどれくらい離れているかを一目で分かるようにしたもので、距離行列と呼ばれます。距離行列を見ると、最も距離が近い二つの群がすぐに分かります。そして、群をまとめるたびに、新しくできた群と残りの群との間の距離を計算し直し、距離行列を更新します。この表を使って、手順を繰り返すことで、最終的に一つの群になるまで計算を進めることができます。
応用例

最長距離法は、様々な分野で活用されています。具体例をいくつか見ていきましょう。
まず、販売促進の分野では、顧客をいくつかの集団に分類するために使われています。顧客の過去の買い物情報や顧客の特徴を示す情報をもとに集団分けすることで、顧客を適切な区分に分けることができます。こうして、それぞれの集団に合った販売戦略を立てることが可能になります。例えば、ある商品を多く購入する集団には、その商品の関連商品を勧めるといった戦略が考えられます。また、特定の属性を持つ集団には、その属性に合わせた広告を配信することで、より効果的な販売促進活動を行うことができます。
次に、画像を扱う分野では、画像の領域分割に役立っています。画像を構成する小さな点の色が似ているかどうかをもとに集団分けすることで、画像の中に写っている別々の物を識別できます。例えば、青空と白い雲が写っている画像では、青い点の集団と白い点の集団に分けることで、空と雲を区別することができます。この技術は、医療画像診断や自動運転技術など、様々な分野で応用されています。
さらに、生物を研究する分野では、生物の分類に用いられています。生物が持つ遺伝子の情報や体の特徴をもとに集団分けすることで、生物同士のつながりを明らかにすることができます。例えば、遺伝子の情報が似ている生物同士は近い仲間であると考えられます。また、体の形が似ている生物同士も、同じ進化の過程をたどってきた可能性が高いと考えられます。このように、最長距離法は生物の進化の歴史を解明する上で重要な役割を果たしています。
このように、最長距離法は情報を整理し、分類する必要がある様々な場面で活用されている、大変有用な手法です。データの種類や目的に合わせて適切に用いることで、様々な分野で新たな発見や効率的な作業につながることが期待されます。
| 分野 | 活用例 | 説明 |
|---|---|---|
| 販売促進 | 顧客の集団分類 | 顧客の過去の買い物情報や顧客の特徴を示す情報をもとに集団分けすることで、顧客を適切な区分に分ける。それぞれの集団に合った販売戦略を立てることが可能。 |
| 画像処理 | 画像の領域分割 | 画像を構成する小さな点の色が似ているかどうかをもとに集団分けすることで、画像の中に写っている別々の物を識別。医療画像診断や自動運転技術などに応用。 |
| 生物学 | 生物の分類 | 生物が持つ遺伝子の情報や体の特徴をもとに集団分けすることで、生物同士のつながりを明らかにする。生物の進化の歴史を解明する上で重要な役割を果たす。 |
利点と欠点

最長距離法には、良い点と悪い点があります。まず、良い点としては、計算の手間が少ないことが挙げられます。集団同士の距離を測るには、単純な距離計算を繰り返すだけで済み、計算にかかる負担が軽いのです。また、小さくまとまった集団を作りやすいことも利点です。
一方、悪い点としては、特殊な値に影響されやすいことが挙げられます。集団同士の距離を測る際に、最も遠い距離を使うため、もし特殊な値があると、その影響を大きく受けて、正しい集団分けができなくなることがあります。例えば、ほとんどのデータが密集しているところに、一つだけ大きく離れたデータがあると、その離れたデータに引っ張られて、集団分けの結果が変わってしまうのです。
また、鎖のように連なった集団には対応しにくいという点も悪い点です。鎖のように連なった集団とは、データが一列に並んでいるような集団のことです。このような集団に対して最長距離法を使うと、うまく分けられないことがあります。例えば、データが数珠つなぎのように連なっている場合、最長距離法では、数珠の両端のデータ間の距離が最も遠いため、その二つのデータを中心とした集団が作られてしまい、本来の集団構造を捉えられないのです。
そのため、データの散らばり方や性質を考えて、最長距離法を使うかどうかを決める必要があります。データが密集していて、特殊な値が少なく、鎖状の集団でない場合は、最長距離法は有効な手法となります。しかし、データが散らばっていたり、特殊な値が多かったり、鎖状の集団である場合は、他の手法を検討する必要があるでしょう。
| 項目 | 内容 |
|---|---|
| 良い点 |
|
| 悪い点 |
|
| 特殊な値への影響 |
|
| 鎖状の集団への対応 |
|
| 最長距離法の適用判断 |
|
