最急降下法:最適化の基礎

AIを知りたい
先生、最急降下法って、どういう意味ですか?なんか、山の頂上を探すのに似てるって聞いたんですけど…

AIエンジニア
そうだね、山の頂上を探すことに似てるけど、最急降下法は、一番低い谷底を探す方法なんだ。山の斜面を一番急な方向に少しずつ下っていくことを想像してみて。それがまさに最急降下法だよ。

AIを知りたい
なるほど!でも、一番低い谷底じゃなかったら、どうするんですか?

AIエンジニア
いい質問だね。実は、最急降下法は、最初に降り始めた場所によって、一番深い谷底にたどり着けないことがあるんだ。小さな谷底に降りてしまって、そこから出られない、そんなイメージだね。だから、最初にどこから降り始めるかが大切なんだよ。
最急降下法とは。
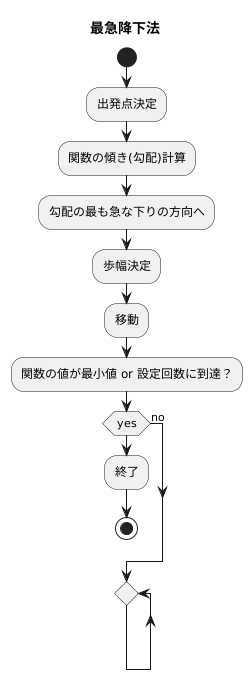
人工知能でよく使われる「最急降下法」について説明します。この方法は、最適な値を見つけるための計算方法である勾配降下法で使われる手順です。まず、初めの値を決めます。そして、その地点での関数の傾きを計算し、最も急な下り坂の方向を見つけます。次に、どのくらい進むのか(移動する幅)を決め、最も急な下り坂の方向に移動します。これを、値が落ち着くまで何度も繰り返します。ただし、この方法では、初めの値の位置によっては、狭い範囲での最小値は見つかりますが、全体で見て一番小さい値は見つからないことがあります。
手法の仕組み

この手法は、ある関数が最小値をとる場所を探すための計算方法です。最も急な下り坂を下ることで谷底を目指す、いわば山登りの逆のような方法です。具体的には、まず探索の出発点を決めます。次に、その地点での関数の傾きを調べます。この傾きは、各変数に対する関数の変化の割合を示すもので、山の斜面の急さを表すものと考えることができます。この傾きが最も急な下りの方向を示しているので、この方向に沿って移動することで関数の値を小さくすることができます。移動する量を歩幅と呼びますが、この歩幅を適切に設定することが大切です。歩幅が大きすぎると最小値を通り過ぎてしまうことがあり、小さすぎると目的の場所にたどり着くまでに時間がかかってしまいます。
この傾きを調べ、歩幅を決めて移動することを繰り返すことで、少しずつ最小値に近づいていきます。ボールが斜面を転がり落ちていくように、関数の値が小さくなっていく様子を想像すると分かりやすいでしょう。
具体的な手順としては、まず関数の傾きを計算します。この傾きは勾配と呼ばれ、各変数に対する関数の変化率を成分とするベクトルで表されます。次に、この勾配を使って現在の位置から移動する方向と量を決定します。移動量は、勾配に学習率と呼ばれる小さな値を掛けたものになります。学習率は、一度の移動でどの程度値を更新するかを制御するパラメータで、適切な値を選ぶことが重要です。小さすぎると収束が遅くなり、大きすぎると最小値を飛び越えてしまう可能性があります。そして、新しい位置で再び関数の勾配を計算し、更新を繰り返します。このプロセスを、関数の値が変化しなくなるか、あらかじめ設定した回数に達するまで続けます。
最適化問題において、この手法は分かりやすく、実装しやすいという利点があります。しかし、大域的な最小値ではなく、局所的な最小値に収束してしまう可能性や、勾配が平坦な領域では収束が遅いといった欠点も存在します。
ステップ幅の決定

坂を下るように一番低い場所を探すことを想像してみてください。この時、一歩の大きさをどれくらいにするかが、『ステップ幅』です。このステップ幅を決めることは、一番低い場所にたどり着くためにとても大切です。
一番低い場所を探す方法の一つに、一番急な方向へ進む方法があります。この方法で進む時、ステップ幅の決め方はいくつかあります。
まず、いつも同じ大きさのステップで進む方法があります。この方法は簡単ですが、ちょうど良いステップ幅を見つけるのが難しいです。もしステップ幅が小さすぎると、なかなか一番低い場所にたどり着けません。逆に大きすぎると、一番低い場所を通り過ぎてしまうかもしれません。
次に、進む方向に沿って一番低い場所を探す方法があります。この方法は、その方向で一番良いステップ幅を見つけられるので、より正確です。しかし、毎回一番良いステップ幅を探すので、計算に時間がかかります。まるで、一歩進むごとに、その方向で一番低い場所を探して、また一歩進むようなものです。
また、状況に応じてステップ幅を変える方法もあります。始めは大きなステップで進み、一番低い場所に近づいてきたら、徐々にステップを小さくしていく方法です。この方法は、早く一番低い場所にたどり着ける可能性があります。
どの方法が良いかは、状況によります。そのため、状況に合わせて適切な方法を選ぶことが大切です。まるで、山を下るのか、丘を下るのかで、適切な一歩の大きさが変わるようなものです。
| ステップ幅決定方法 | 説明 | メリット | デメリット |
|---|---|---|---|
| 固定ステップ幅 | 常に一定のステップ幅で進む | 簡単 | 適切なステップ幅の設定が難しい。小さすぎると時間がかかり、大きすぎると最適解を通り過ぎる可能性がある。 |
| 直線探索 | 進む方向に沿って一番低い場所を探し、その地点まで進む | より正確なステップ幅決定が可能 | 計算に時間がかかる |
| 可変ステップ幅 | 状況に応じてステップ幅を調整。最初は大きく、徐々に小さくする | 早く最適解にたどり着く可能性がある | 調整方法の設計が必要 |
初期値の影響

最急降下法という計算方法は、最初の値の設定によって結果が大きく変わってしまうという、大切な性質を持っています。例えるなら、山登りで山頂を目指すとしましょう。山頂にたどり着けるかどうかは、どこから登り始めるか、つまり出発地点によって大きく変わるのと同じです。
もし最初の値が適切であれば、全体を見たときに最も低い地点、いわば最も深い谷底のような場所(大域的最小値)にたどり着くことができます。しかし、最初の値が適切でないと、局所的な最小値、つまり比較的小さな谷(極小値)で止まってしまうことがあります。これは、山に複数の谷がある場合、出発地点によっては最も深い谷底にたどり着けないのと同じです。
計算の対象となる関数の形によっては、このような小さな谷がたくさん存在する可能性があり、どの谷にたどり着くかは、最初の値に左右されます。ですから、最急降下法を使う際には、最初の値を適切に選ぶことがとても重要になります。
より良い結果を求めるためには、いくつもの異なる出発地点から計算を始めて、それぞれで得られた結果を比べるという方法も有効です。複数の谷を探索することで、最も深い谷底、つまり最も良い解を見つけられる可能性が高まります。この方法は、まるで複数の登山ルートを試して、一番早く山頂にたどり着くルートを探すようなものです。
手法の限界

最急降下法は、分かりやすく、取り入れやすい最適化手法として知られています。しかし、いくつかの弱点も抱えています。まず、最初の値によって結果が大きく変わる点が挙げられます。つまり、全体で最も低い値ではなく、局所的に低い値に落ち着いてしまう可能性があります。山を想像してみてください。全体で最も低い谷底ではなく、近くの小さな谷で立ち止まってしまうようなものです。
次に、値にたどり着くまで時間がかかる場合があります。特に、複雑な形をした関数や、傾きが緩やかな場所では、最低値に到達するまでに何度も計算を繰り返す必要があります。これは、緩やかな坂道をゆっくりと下っていくようなものです。なかなか目的地にたどり着けません。
さらに、平坦な場所で探索が止まってしまうという問題もあります。傾きがゼロになる平坦な場所では、それ以上進むべき方向が分からなくなり、探索が停止してしまいます。これは、広大な平原で方向を見失い、目的地にたどり着けないようなものです。このような平坦な領域は「台地」とも呼ばれます。
これらの弱点を克服するために、最急降下法を改良した様々な方法が考え出されています。例えば、「勢いをつける方法」や「共役勾配法」は、最急降下法よりも早く値にたどり着くように工夫されています。また、「確率的勾配降下法」は、大量のデータに対しても効率よく最適化を行うことができます。これらの改良された手法は、より早く、より確実に最低値を見つけるための工夫が凝らされています。
| 弱点 | 説明 | 例え |
|---|---|---|
| 初期値依存性 | 初期値によって結果が大きく変わり、局所的な最小値に陥る可能性がある。 | 全体で最も低い谷底ではなく、近くの小さな谷で立ち止まるようなもの。 |
| 収束速度の遅さ | 複雑な関数や傾きが緩やかな場所では、最小値到達までに時間がかかる。 | 緩やかな坂道をゆっくりと下っていくようなもの。 |
| 平坦な領域での停止 | 傾きがゼロの平坦な場所(台地)で探索が停止する。 | 広大な平原で方向を見失い、目的地にたどり着けないようなもの。 |
他の手法との比較

最適化問題を解くための方法は、最急降下法以外にも数多く存在します。それぞれの手法には得意な問題や不得意な問題、計算の手間など、様々な違いがあります。適切な方法を選ぶためには、それらの特徴を理解することが重要です。ここでは、最急降下法とよく比較される代表的な手法をいくつか紹介します。
まず、ニュートン法は、関数の形をより精密に捉えることで、最急降下法よりも速く最適な値にたどり着くことができます。これは、坂道を下る際に、傾きだけでなく、坂道の曲がり具合も考慮するようなイメージです。しかし、この曲がり具合を計算するには、多くの計算資源が必要となります。そのため、扱う問題の規模が大きい場合は、計算に時間がかかりすぎてしまうことがあります。
次に、準ニュートン法は、ニュートン法の考え方を参考に、計算の手間を減らした方法です。坂道の曲がり具合を完全に計算するのではなく、近似的に求めることで、計算の負担を軽減しています。これにより、ニュートン法ほど速くはないものの、最急降下法よりは速く、かつ計算資源の消費も抑えることができます。
また、共役勾配法も最急降下法の改良版と言える方法です。特に、変数が非常に多い高次元の問題に効果を発揮します。過去の探索方向を記憶しながら進むことで、より効率的に最適な値を探し出します。
さらに、遺伝的アルゴリズムや焼きなまし法といった、メタヒューリスティクスと呼ばれる手法も存在します。これらの手法は、生物の進化や物質の冷却といった自然現象を模倣することで、複雑な問題の最適解を見つける可能性を高めます。ただし、一般的に計算コストは高く、最適解の保証はありません。
最急降下法は、これらの手法と比べると、計算方法が単純で理解しやすく、実装も容易です。そのため、最適化の基礎となる重要な手法と言えるでしょう。ただし、問題によっては収束が遅い場合もあります。他の手法と比較検討し、問題の特性に合わせて最適な手法を選択することが重要です。
| 手法 | 特徴 | メリット | デメリット |
|---|---|---|---|
| 最急降下法 | 傾きを利用して最適値を探す | 計算が単純、理解しやすく実装が容易 | 問題によっては収束が遅い |
| ニュートン法 | 傾きと曲がり具合を利用 | 最急降下法より速く最適値に到達 | 計算資源が多く必要、大規模問題には不向き |
| 準ニュートン法 | ニュートン法の計算を簡略化 | ニュートン法より計算資源の消費が少ない、最急降下法より速い | ニュートン法ほど速くない |
| 共役勾配法 | 過去の探索方向を記憶 | 高次元の問題に効果的 | – |
| 遺伝的アルゴリズム、焼きなまし法 | 自然現象を模倣 | 複雑な問題の最適解を見つける可能性が高い | 計算コストが高い、最適解の保証がない |
