最急降下法:最適化への近道

AIを知りたい
先生、最急降下法ってどういう意味ですか?

AIエンジニア
そうですね、最急降下法は、一番急な坂道を下るようにして、一番低い場所を探す方法です。 例えば、ボールを山の上から転がすと、一番低い谷底に落ち着きますよね。最急降下法も似たようなことをしています。

AIを知りたい
谷底のような一番低い場所を探すというのはどういうことですか?

AIエンジニア
AIの世界では、色々な値を調整して一番良い結果を見つけたい場合があります。その「一番良い結果」に対応する場所を一番低い谷底、調整する値を山の斜面の位置だと考えて、一番低い谷底を探す、つまり一番良い結果を見つけるのに、最急降下法を使うんです。ただし、谷が複数ある場合、一番低い谷底ではなく、近くの谷底で止まってしまうこともあるので注意が必要です。
最急降下法とは。
人工知能で使われる言葉の一つに「最急降下法」というものがあります。これは、一番良い値を見つけるための方法である勾配降下法で使われる手順のことです。まず、最初の値を決めます。次に、その場所での関数の傾きを計算し、一番急な下り坂の方向を見つけます。そして、どのくらい進むか(移動する幅)を決めて、一番急な下り坂の方向に移動します。これを繰り返し、値が変化しなくなるまで続けます。ただし、最初の値の場所が悪いと、全体で一番小さい値ではなく、その近辺で一番小さい値しか見つからないことがあります。
はじめに

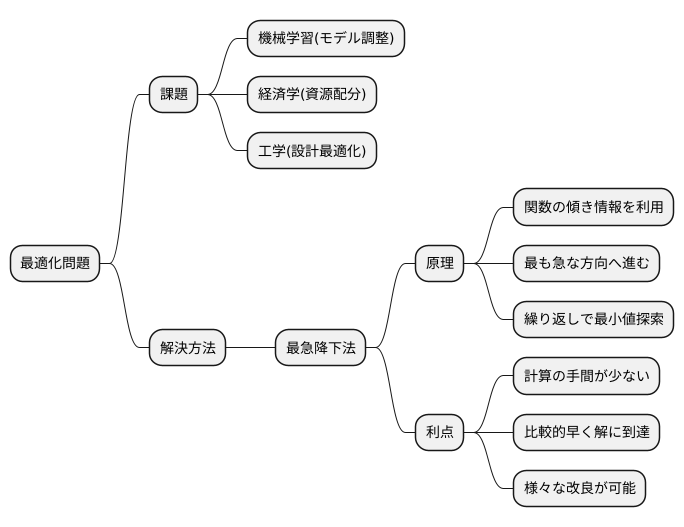
あらゆる分野で、最も良い結果を得るための方法を見つける、すなわち最適化問題は重要な課題です。例えば、機械学習では、学習モデルの精度を上げるために、モデルの調整を行います。経済学では、限られた資源を最大限に活用するために資源配分を最適化します。工学では、性能を最大化し、コストを最小化するために設計の最適化を行います。このように、最適化が必要な場面は様々です。
これらの最適化問題を効率よく解くために、様々な計算方法が開発されてきました。その中でも、最急降下法は基本的な手法として広く使われています。この手法は、関数の傾き情報を使って、最適な解へと効率的に近づくことを目指します。山の斜面を下る様子を想像してみてください。最も急な方向へと進んでいくことで、谷底、つまり最小値にたどり着きます。最急降下法もこれと同じように、現在の位置における傾きを計算し、その反対方向へと進むことを繰り返すことで、最小値を探し出します。
この計算方法は単純ですが、多くの最適化問題で効果を発揮する強力な手法です。計算の手間が少なく、比較的早く解にたどり着けるため、最初の試行として最適です。さらに、様々な改良を加えることで、より複雑な問題にも対応できます。この手法を理解することは、最適化問題を解く上で重要な一歩となります。
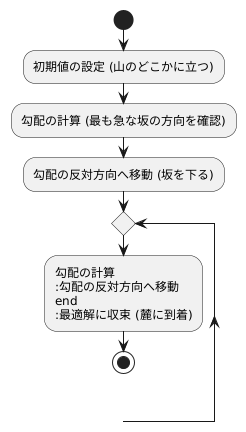
計算手順

この計算手順は、山の頂上から麓へ向かう人の動きに例えることができます。まず、人は山のどこかに立ちます。これが初期値の設定にあたります。次に、周囲を見渡し、最も急な坂の方向を確認します。これが勾配の計算にあたります。そして、その坂を下るように移動します。これが勾配の反対方向への移動にあたります。一歩の大きさがステップ幅に相当し、大きすぎると谷底を通り過ぎてしまうかもしれませんし、小さすぎると麓へたどり着くまでに時間がかかります。適切な一歩の大きさで、坂を下る動作を繰り返すことで、最終的には麓にたどり着くことができます。これが最適解への収束にあたります。
もう少し詳しく説明すると、初期値とは、最適な値を探すための最初の値のことです。この値は適当に決めても構いませんが、問題によっては適切な初期値を選ぶことで計算速度が向上することがあります。勾配は、現在の位置から少しだけ値を変えたときに、関数の値がどれくらい変化するかを表すものです。変化量が正であれば関数の値は増加し、負であれば減少します。勾配を求めるためには微分という計算を行います。ステップ幅は、一度の移動でどれだけの距離を進むかを調整する値です。小さすぎると最適な値にたどり着くまでに多くの計算が必要になり、大きすぎると最適な値を通り過ぎてしまう可能性があります。
最適なステップ幅は問題によって異なり、試行錯誤によって最適な値を見つけることが一般的です。これらの手順を繰り返すことで、関数の値が徐々に小さくなり、最終的には最適な値に近づいていきます。関数の値が変化しなくなったら、あるいはあらかじめ決めた回数だけ繰り返したら計算を終了します。このように、最急降下法は直感的な手順で最適な値を求めることができるため、様々な分野で広く利用されています。
長所と短所

最急降下法には、手軽に使えるという大きな利点があります。この手法は、まるで山の斜面を下るように、現在地の傾きが最も急な方向へ進むことを繰り返すことで、関数の最小値を探し出す方法です。この計算手順は非常に単純で、プログラムに落とし込むのも容易です。そのため、専門的な知識がなくても比較的簡単に実装できます。さらに、一回の計算に必要な処理が少ないため、計算にかかる負担も軽く済みます。この特徴から、膨大なデータを扱う大規模な問題にも対応できる、使い勝手の良い手法と言えるでしょう。
しかし、最急降下法には、落とし穴も存在します。関数の形が複雑で、複数の谷がある場合、出発点によっては局所的な最小値に捕らわれてしまうことがあります。まるで深い谷底に迷い込んだ登山家のように、全体を見渡せず、真の最小値にたどり着けない可能性があるのです。さらに、最小値に近づく速度が遅いケースも見られます。特に、谷が細長く伸びている場合、まるで底の見えない細い道をゆっくりと下っていくように、最適な解にたどり着くまでに多くの時間を要することがあります。
このような欠点を解消するために、様々な改良が加えられています。例えば、慣性の概念を導入することで、局所解に陥る危険性を減らし、より効率的に最小値を探す方法などが研究されています。これらの改良は、最急降下法の弱点を補い、より幅広い問題に適用できる強力な道具へと進化させています。
| 項目 | 内容 |
|---|---|
| 利点 | 手軽に使える 計算手順が単純 実装が容易 計算負荷が軽い 大規模問題に対応可能 |
| 欠点 | 局所解に陥る可能性 収束速度が遅い場合がある |
| 改良 | 慣性の概念の導入など |
ステップ幅の調整

最急降下法は、目的関数の値を最小にするために広く使われている手法です。この手法は、現在地点から目的関数が最も大きく減少する方向へ、一定の幅(ステップ幅)で移動することを繰り返すことで、最適解を探します。このステップ幅の調整は、最急降下法の性能を左右する重要な要素であり、適切な値を選ぶ必要があります。
ステップ幅が大きすぎるとどうなるでしょうか。山を下ることを想像してみてください。一歩が大きすぎると、谷底を飛び越えてしまい、反対側の斜面を登ってしまうかもしれません。最急降下法でも同様に、大きすぎるステップ幅は最適解を通り過ぎてしまい、解が振動したり、最悪の場合、発散してしまう可能性があります。これは、計算の失敗につながるだけでなく、貴重な計算時間を無駄にしてしまうことにもなります。
逆に、ステップ幅が小さすぎるとどうなるでしょうか。今度は、一歩一歩が小さすぎて、谷底へなかなかたどり着けない状態を想像してみてください。最急降下法においても、小さすぎるステップ幅は収束速度を遅くし、計算時間が長くなってしまうという問題を引き起こします。目的関数によっては、計算が終わるまでに膨大な時間がかかってしまうかもしれません。
では、どのように適切なステップ幅を選べば良いのでしょうか。残念ながら、最適なステップ幅は扱う問題の性質に依存するため、万能な値はありません。そのため、様々なステップ幅調整の手法が提案されています。例えば、常に一定のステップ幅を用いる方法や、各ステップで最適なステップ幅を探索する直線探索法、Armijo ruleなどを用いる方法などがあります。これらの手法を問題に合わせて適切に使い分けることで、最急降下法の性能を向上させることができます。どの手法が最適かは、試行錯誤によって見つけることが重要です。
| ステップ幅 | 結果 | 問題点 |
|---|---|---|
| 大きすぎる | 最適解を通り過ぎる、解が振動する、発散する | 計算の失敗、計算時間の無駄 |
| 小さすぎる | 収束速度が遅い | 計算時間が長い |
適切なステップ幅の決定方法: 問題に依存するため、万能な値はない。
ステップ幅調整手法の例:
・一定のステップ幅を用いる方法
・各ステップで最適なステップ幅を探索する直線探索法
・Armijo ruleなどを用いる方法
応用例

最急降下法は、様々な分野で活用されている汎用的な最適化手法です。目的関数の値を最小化する最適な解を見つけるために、関数の勾配に基づいて探索を行います。この手法は、広範囲な問題に適用できるため、多くの分野で重要な役割を担っています。
機械学習の分野では、最急降下法はニューラルネットワークの学習において中心的な役割を果たします。ニューラルネットワークは、入力データから出力データを予測する複雑な関数で表現されます。この関数の内部には、多数のパラメータが存在し、これらのパラメータを調整することで、予測精度を向上させることができます。最急降下法は、予測誤差を最小化するようにパラメータを更新することで、最適なパラメータ値を探索します。具体的には、損失関数と呼ばれる予測誤差の指標を用いて、その勾配を計算し、勾配の負の方向にパラメータを更新します。このプロセスを繰り返すことで、徐々に最適なパラメータに近づき、モデルの精度を高めることができます。
画像処理の分野でも、最急降下法は様々な用途で利用されています。例えば、画像のノイズ除去では、ノイズを含んだ画像を滑らかにするために、画像を表現する関数の勾配を用いてノイズ成分を低減します。画像の鮮明化や特定の特徴抽出にも、最急降下法が活用されます。画像のエッジ(輪郭)を強調する処理や、特定のテクスチャを抽出する処理など、様々な画像処理タスクにおいて、勾配に基づいた最適化は効果的です。
制御工学の分野では、制御システムの最適化に最急降下法が応用されます。制御システムは、目標値に追従するように対象を制御する仕組みです。例えば、ロボットアームの軌跡制御や温度制御などが挙げられます。最急降下法を用いることで、制御対象のモデルに基づいて、制御性能を最適化するパラメータを探索することができます。制御パラメータを調整することで、より速く、より正確に目標値に到達する制御システムを実現できます。
このように、最急降下法は様々な分野で重要な最適化手法として活躍しています。勾配に基づいて解を探索するというシンプルな原理ながらも、幅広い問題に適用できる柔軟性と強力さを持ち、多くの応用で成果を上げています。
| 分野 | 最急降下法の適用例 | 詳細 |
|---|---|---|
| 機械学習 | ニューラルネットワークの学習 | 予測誤差を最小化するようにパラメータを更新し、最適なパラメータ値を探索。損失関数の勾配を用いて、勾配の負の方向にパラメータを更新。 |
| 画像処理 | ノイズ除去、鮮明化、特徴抽出 | ノイズを含んだ画像を滑らかにするために勾配を用いてノイズ成分を低減。エッジ強調や特定テクスチャ抽出にも活用。 |
| 制御工学 | 制御システムの最適化 | 制御対象のモデルに基づいて、制御性能を最適化するパラメータを探索。より速く、より正確に目標値に到達する制御を実現。 |
まとめ

最適な答えを見つけるための手法の中で、最も基本的な方法の一つが最急降下法です。この方法は、山の斜面を下るように、現在地から最も急な方向へ少しずつ進んでいくことで、一番低い谷底(最適解)を目指すという考え方です。イメージとしては、ボールを転がして一番低い場所を探すようなものです。
この方法は、比較的簡単な計算で実現できるため、多くの場面で使われています。まるで、道案内人が「こっちが下り坂ですよ」と教えてくれるように、現在の位置での傾き情報だけを使って次の進むべき方向を決めるので、複雑な計算は必要ありません。そのため、計算にかかる時間も短く済むという利点があります。
しかし、最急降下法には弱点も存在します。例えば、山には谷底が複数ある場合があります。この場合、ボールは一番低い谷底ではなく、たまたま近くに小さな谷底に落ち込んでしまう可能性があります。これが、局所解と呼ばれる問題です。また、斜面が緩やかな場所では、なかなか谷底に辿り着かず、時間がかかってしまうこともあります。これは、収束速度の問題です。
これらの弱点を克服するために、一歩進む距離(ステップ幅)を調整することが重要になります。一歩が大きすぎると、最適解を通り過ぎてしまう可能性があり、小さすぎると、なかなか目的地に辿り着きません。ちょうど良いステップ幅を見つけることで、より早く、より正確に最適解に近づくことができます。
最急降下法は、機械学習や画像処理、ロボットの制御など、様々な分野で活用されています。例えば、機械学習では、予測モデルの精度を上げるために、最急降下法を使って最適なパラメータを探し出します。このように、最急降下法は、様々な問題を解決するための重要な道具として、なくてはならないものとなっています。今後も、更なる改良や、新たな応用が期待されています。
| 手法名 | 概要 | 利点 | 欠点 | 対策 | 応用例 |
|---|---|---|---|---|---|
| 最急降下法 | 山の斜面を下るように、現在地から最も急な方向へ少しずつ進んでいくことで、一番低い谷底(最適解)を目指す。 |
|
|
ステップ幅の調整 |
|
