深さ優先探索で迷路を解く

AIを知りたい
先生、「深さ優先探索」って、どういう探索方法ですか?迷路を解くときみたいに、行き止まりまで行って戻って、また別の道を探していくんですよね?

AIエンジニア
そうだね。まさに迷路を解くときみたいに、まず一つの道をずーっと進んでいくんだ。行き止まりにぶつかったら、一つ前の分かれ道まで戻って、まだ進んでいない別の道を探していく探索方法だよ。

AIを知りたい
なるほど。でも、そうやって探していくと、遠回りになっちゃったりしませんか?

AIエンジニア
いいところに気がついたね。その通りで、深さ優先探索は必ずしも一番短い道で見つかるわけではないんだ。でも、あまり記憶する場所を使わないから、複雑な迷路でも解きやすいという利点があるんだよ。
深さ優先探索とは。
人工知能に関係する言葉である「深さ優先探索」について説明します。これは、コンピュータで迷路を解くとき、まず始点から順番に道を探していく方法です。道が行き止まりになったら、一つ前の分かれ道に戻って、別の道を探します。これを繰り返して、ゴールまでの道筋を見つけます。この方法は、他の探し方と比べて、コンピュータの記憶領域をあまり使いません。なぜなら、行き止まりになったらすぐに戻って別の道を探せば良いからです。ただし、ゴールまでの道筋が見つかっても、それが一番短い道筋とは限りません。
深さ優先探索とは

深さ優先探索は、複雑な問題を解き明かすための、まるで迷路を解くような手法です。コンピュータの世界では、様々な問題を、点と線でできた図形、つまりグラフと呼ばれる形で表すことができます。このグラフは、点を節、線を辺と呼びます。たとえば、迷路は、通路を辺、分岐点や行き止まりを節として表すことができます。深さ優先探索は、このグラフの節を一つずつ調べていく方法です。出発点から始めて、可能な限り深く、行き止まりになるまで進んでいきます。まるで迷路の中で、一本道を突き進んでいくようなイメージです。行き止まりにたどり着いたら、一つ前の分岐点まで戻り、まだ進んでいない道があれば、そこから再び深く進んでいきます。これを繰り返すことで、最終的に目的の場所にたどり着くことができます。
たとえば、宝探しゲームを考えてみましょう。迷路のような地図上に宝が隠されていて、あなたは出発点から宝を探し始めます。深さ優先探索を使うと、まず一つの道を可能な限り深く進んでいきます。行き止まりにぶつかったら、一つ前の分岐点に戻り、まだ探索していない道があれば、そちらへ進んでいきます。これを繰り返すことで、最終的に宝を見つけ出すことができます。深さ優先探索は、このように行き止まりまで進んでから引き返し、別の道を試すという動作を繰り返すため、迷路探索に非常に適しています。また、この方法は、パズルを解いたり、家系図をたどったり、コンピュータネットワークの経路を調べたりと、様々な場面で活用されています。深さ優先探索は、その分かりやすさと効率性から、広く使われているのです。まるで迷路を解くように、複雑な問題を一つずつ紐解いていく、頼もしい探索方法と言えるでしょう。
探索の手順

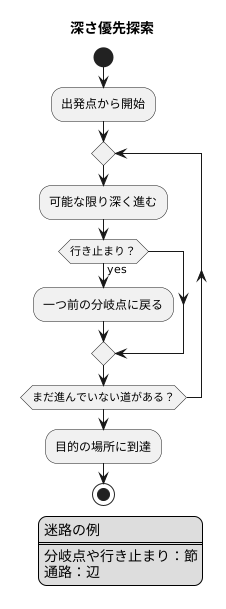
探索は、まるで迷路を解くようなものです。深さ優先探索と呼ばれる方法を見てみましょう。この方法は、まず出発地点を決めることから始まります。迷路の入り口のようなものです。そこから伸びる道を一つ選び、先へ進みます。この時、通った道に印をつけて、既に通ったことを覚えておきます。
次に、進んだ先からまた道を選び、さらに奥へと進んでいきます。これを繰り返すことで、迷路の奥深くまで調べることができます。まるで一本道を突き進むように探索を進めます。もし行き止まりにぶつかった場合は、一つ前に戻り、まだ通っていない道があれば、そこから再び探索を始めます。この戻る動作が、深さ優先探索の大切なところです。
行き止まりにぶつかって戻ることを繰り返しながら、迷路のすべての道を調べます。すべての道が探索済みになったら、探索は終わりです。もし迷路の出口、つまり目標地点に辿り着いたら、探索は成功です。入り口から出口までの経路が、迷路の解となります。
例として、木の枝を想像してみましょう。幹から枝が伸び、さらに小さな枝が伸びています。深さ優先探索は、まず一つの枝を根元から先端まで辿ります。先端まで行ったら、一つ前の分かれ点に戻り、まだ調べていない枝があれば、そちらを辿ります。すべての枝を調べ終わるまで、これを繰り返します。まるで木の枝を一本ずつ丁寧に調べていくような探索方法です。
利点と欠点

深さ優先探索は、まるで迷路を解くように、一つの道を可能な限り深く進んでから、行き止まりに達したら引き返して別の道を進む探索方法です。この探索方法には、長所と短所があります。
まず、長所について考えてみましょう。深さ優先探索の大きな利点の一つは、使用する記憶場所が少ないことです。探索を進める際には、現在進んでいる道筋の情報だけを覚えておけば十分です。迷路全体の形を記憶しておく必要はありません。これは、非常に大きな迷路や複雑な経路を探索する場合に、大きな助けとなります。記憶場所の使用量が少ないため、計算機の負担を軽くできるのです。また、深さ優先探索は、プログラムで書きやすいため、比較的簡単に実現できます。特に、繰り返し処理を繰り返す仕組みを使うと、簡潔に表現できます。
次に、短所について見ていきましょう。深さ優先探索は、必ずしも一番短い道筋を見つけられるとは限りません。これは、深さ優先探索の性質上、とにかく深く掘り下げていくため、回り道をして目的地にたどり着く可能性があるからです。たとえば、迷路の入り口付近に近道があったとしても、深さ優先探索ではまず遠くの行き止まりまで進んでから、近道に気づくことになります。また、迷路に円を描くように道がつながっている部分(ループ)があると、永遠に同じ道を回り続けてしまう可能性があります。そのため、ループに陥らないように注意深くプログラムを作成する必要があります。行き止まりやループを適切に処理しないと、探索が完了しない可能性があるため、注意深く対策を施す必要があります。
| 項目 | 内容 |
|---|---|
| 長所 | 記憶場所が少ない プログラムで書きやすい |
| 短所 | 最短経路を見つけられるとは限らない ループに陥る可能性がある |
幅優先探索との比較

よく似た探索方法である深さ優先探索と幅優先探索には、それぞれ違った特徴があります。どちらもグラフや木構造といった繋がりを持ったデータ構造を探索する際に用いられますが、その進み方が大きく異なります。
深さ優先探索は、まるで迷路を進むように、行き止まりにぶつかるまでひたすら奥深く進んでいく探索方法です。一方、幅優先探索は、出発点から近い場所を順に調べていく探索方法です。例えるなら、池に石を投げ入れた際に、波紋が広がっていく様子に似ています。中心から外側へ、同心円状に探索範囲を広げていきます。
この二つの探索方法の大きな違いは、探索の順序にあります。深さ優先探索は、とにかく深く掘り下げていくため、出発点から遠く離れた場所を先に探索することがあります。一方、幅優先探索は、出発点に近い場所から順に探索していくため、目的地までの最短経路を必ず見つけることができます。これは幅優先探索の大きな利点です。
しかし、幅優先探索には欠点もあります。探索範囲が広がるにつれて、既に調べた場所の情報を記憶しておく必要があり、多くの記憶領域が必要になります。深さ優先探索では、現在探索中の経路の情報だけを覚えておけば良いので、記憶領域の消費は少なくて済みます。
結局のところ、どちらの探索方法が適しているかは、解きたい問題の種類や利用できる計算機の性能によって変わってきます。もし最短経路を見つけることが重要で、かつ計算機の記憶容量に余裕があるならば、幅優先探索が適しています。一方、記憶容量が限られている場合や、最短経路である必要がない場合は、深さ優先探索の方が適していると言えるでしょう。
| 項目 | 深さ優先探索 | 幅優先探索 |
|---|---|---|
| 探索方法 | 行き止まりまで深く進む | 出発点から近い場所を順に調べる |
| イメージ | 迷路 | 池の波紋 |
| 探索順序 | 出発点から遠くても先に探索 | 出発点に近い場所から順に探索 |
| 最短経路 | 必ずしも見つけられない | 必ず見つける |
| メモリ使用量 | 少ない | 多い |
| 利点 | メモリ消費が少ない | 最短経路を見つけられる |
| 欠点 | 最短経路を見つけられない場合がある | メモリ消費が多い |
| 適した状況 | メモリ容量が少ない場合、最短経路が不要な場合 | 最短経路が必要な場合、メモリ容量に余裕がある場合 |
応用例

深さ優先探索は、様々な場面で活用される、とても便利な方法です。まるで木の枝を辿るように、まず一つの道筋を奥深くまで進んでいきます。行き止まりにぶつかったら、一つ前に戻って別の道を探し、これを繰り返すことで、あらゆる可能性を調べ尽くすことができます。
この方法は、迷路を解くのに役立ちます。迷路の入り口からスタートし、分かれ道に差し掛かるたびに、どれか一つの道を選びます。行き止まりに辿り着いたら、一つ前の分かれ道まで戻り、別の道を選びます。これを繰り返すことで、迷路の出口に辿り着くことができます。
また、パズルゲームの攻略にも、この深さ優先探索が役立ちます。例えば、数当てゲームなどで、どの数字を選ぶべきか迷った時、まず一つの数字を選び、その結果を見て次の数字を選びます。間違った数字を選んだ場合は、一つ前の段階に戻り、別の数字を選びます。これを繰り返すことで、正解に辿り着くことができます。
さらに、囲碁や将棋のようなゲームでも、この考え方は使われています。コンピュータは、可能な手を一つずつ順番に深く掘り下げて考えていきます。そして、その先にある有利な局面を探し、最も良い手を選びます。まるで、何手も先を読んで、最善の一手を打つ名人のようです。
人の繋がりを調べる時にも、深さ優先探索は役立ちます。例えば、ある人から始めて、その人の友達、さらにその友達の友達と、繋がりを辿っていくことで、どの程度の人と繋がっているのか、どのようなグループを形成しているのかを知ることができます。
このように、深さ優先探索は、様々な問題を解くための、とても強力な道具なのです。問題を解く手順を一つずつ深く掘り下げて調べるという基本的な考え方は、色々な場面で応用できます。そして、この方法は、コンピュータの力を借りて複雑な問題を解く際に、特に役立ちます。
Pythonでの実装例

深さ優先探索は、汎用性の高い探索手法であり、Pythonを使うと比較的容易にプログラムに落とし込むことができます。ここでは、Pythonを使って深さ優先探索を行う方法について、具体的な例を挙げながら説明します。
まず、深さ優先探索の基本的な考え方を確認しましょう。深さ優先探索では、出発点から可能な限り深く探索を進めます。行き止まりに達した場合、一つ前に戻って別の道を探索します。これを繰り返すことで、最終的に目標地点に到達するか、全ての経路を探索し尽くします。
Pythonで深さ優先探索を実装する際には、再帰関数を用いると便利です。再帰関数は自分自身を呼び出す関数であり、深さ優先探索の動作と相性が良いため、コードを簡潔に記述することができます。
具体的な例として、二次元の迷路を解くプログラムを考えてみましょう。迷路は二次元配列で表現し、壁と通路をそれぞれ異なる値で表します。探索の開始地点と目標地点も配列上で指定します。
プログラムは、現在位置から上下左右の隣接するマスを順番に探索します。未探索の通路が見つかった場合、そのマスを現在位置として再帰関数を呼び出します。壁にぶつかった場合や、既に探索済みのマスに到達した場合は、探索を打ち切って一つ前のマスに戻ります。このようにして、迷路の全ての通路を隈なく探索していきます。
実際のプログラムでは、各マスの状態(未訪問、訪問済み、行き止まり)を記録する必要があります。これにより、同じマスを何度も探索することを避け、探索の効率を高めることができます。
Pythonのリストや辞書を用いることで、迷路の状態を容易に管理できます。また、再帰関数の呼び出し回数に上限を設定することで、無限ループに陥ることを防ぐことも重要です。
このように、Pythonを用いることで、深さ優先探索を比較的容易に実装することができます。迷路以外にも、グラフ探索などの様々な問題に応用できますので、是非試してみてください。