幅優先探索で迷路を解く

AIを知りたい
先生、『幅優先探索』って、どういう探索方法か教えてください。

AIエンジニア
そうですね。迷路で例えると、スタート地点から行ける場所を全部まず探します。そこからまた行ける場所を全部探す、というように、順番に広げていく探索方法です。必ず最短ルートを見つけられるのが特徴ですね。

AIを知りたい
なるほど。でも、全部の場所を覚えておかないといけないから、広い迷路だと大変そうですね。

AIエンジニア
その通りです。記憶しておく場所が多くなりすぎて、コンピュータの容量が足りなくなる可能性があるのが欠点ですね。迷路が複雑になればなるほど、たくさんの場所を覚えておかなければならないので。
幅優先探索とは。
人工知能の用語で『幅優先探索』というものがあります。これは、コンピュータで迷路を解くとき、どのように道をたどるかを決める方法のひとつです。
迷路を解くことを考えてみましょう。まずスタート地点から、行ける道を順番に調べていきます。このとき、どの道を先に調べるかで、ゴールまでの道のりや、かかる時間が変わってきます。幅優先探索では、スタート地点から近い場所を優先的に調べていきます。つまり、スタートから近い順に、あらゆる方向へ順番に広げていくイメージです。この方法だと、ゴールまでの最短ルートを必ず見つけることができます。
しかし、この方法には欠点もあります。これまで通ってきた道をすべて覚えておかなければならないため、迷路が複雑になると、覚えておくべき情報が多すぎて、コンピュータの容量が足りなくなり、処理を続けられなくなることがあるのです。
迷路と探索

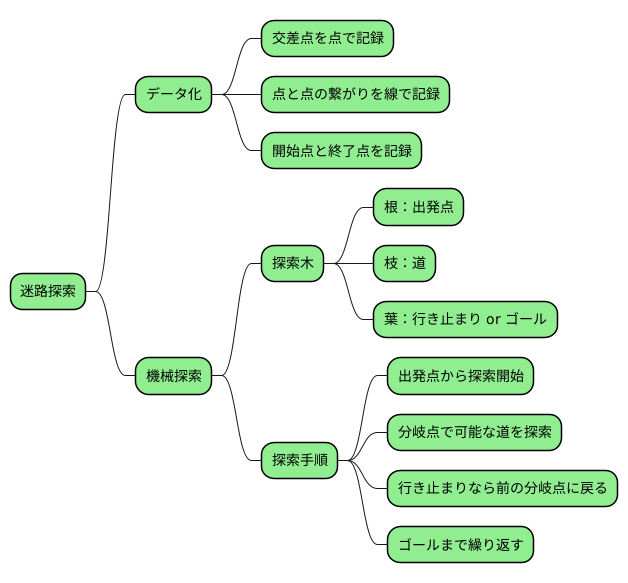
複雑に入り組んだ道と、たった一つの正解への道筋を持つ迷路。これを機械に解かせるにはどうすれば良いのでしょうか。人のように目で見て考えることができない機械のために、迷路をデータの形に変換する必要があります。迷路は、縦横に交差する道と壁でできています。この構造を、点と線で表現してみましょう。まず、道の交わる点を一つずつデータとして記録します。次に、どの点と点が線で繋がっているか、つまり道で繋がっているかを記録します。そして、迷路の始まりと終わりとなる二つの特別な点も記録します。これで、機械が理解できる形で迷路を表現できました。
機械は、記録された迷路のデータに基づいて、出発点から探索を始めます。まるで、一本の木が枝分かれしていくように、一つ一つの分岐点ですべての可能な道を探っていきます。これは、木の根っこが出発点、枝が道、そして葉が行き止まり、またはゴール地点となる木のような図で表すことができます。この図を探索木と呼びます。探索木を使うことで、機械が迷路をどのように探索しているのかを視覚的に捉えることができます。もし、行き止まりに辿り着いたら、一つ前の分岐点に戻り、まだ進んでいない別の道を探索します。これをゴールに辿り着くまで繰り返します。まるで、迷路の中で糸を手繰るように、機械は一つずつ道を辿り、最終的にゴールへの道筋を見つけ出すのです。このように、迷路の探索は、複雑な問題を一つずつ分解し、順序立てて解いていくという、機械の得意とする作業の一つなのです。
幅優先探索とは

道に迷ったとき、どのようにして目的地を探しますか?色々な探し方があると思いますが、その中でも基本的な方法の一つに、幅優先探索という考え方があります。幅優先探索とは、出発点から近い場所を優先的に探していく方法です。
例えば、迷路を考えてみましょう。あなたは迷路の入り口に立っていて、出口を探しています。この時、幅優先探索を使うと、まず入り口に隣接する通路を全て調べます。行き止まりだったら引き返して、まだ調べていない通路に進みます。次に、入り口から二歩でたどり着ける場所を全て調べます。そして、三歩でたどり着ける場所、四歩でたどり着ける場所…と、順番に探していくのです。ちょうど、池に石を投げ入れた時に、波紋が広がっていく様子を想像してみてください。石が落ちた場所から、同心円状に波紋が広がっていくように、探索範囲を広げていくのが幅優先探索です。
この探索方法には、大きな利点があります。それは、最短経路で目的地にたどり着く解を必ず見つけることができるという点です。入り口から近い順に探しているので、出口が見つかった時は、それが最短経路になっていることが確実です。回り道をして出口にたどり着くよりも、最短距離で出口を見つけたいですよね。
もちろん、幅優先探索にも欠点があります。それは、探索範囲が広がると、調べなければならない場所の数が非常に多くなる可能性があるということです。特に、迷路が複雑な場合や、出口が入り口から遠い場所にある場合は、多くの時間を要するかもしれません。しかし、最短経路を確実に見つけるという点では、非常に有効な探索方法と言えるでしょう。
| 探索方法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 幅優先探索 | 出発点から近い場所を優先的に探す。池に石を投げた時の波紋のように、同心円状に探索範囲を広げる。 | 最短経路で目的地にたどり着く解を必ず見つけることができる。 | 探索範囲が広がると、調べなければならない場所の数が非常に多くなる可能性がある。特に、迷路が複雑な場合や、出口が入り口から遠い場所にある場合は、多くの時間を要する。 |
幅優先探索の弱点

幅優先探索は、出発点から近い順に探索を行うという方法で、最短経路を見つけるのに役立ちます。しかし、この探索方法には重大な欠点も存在します。それは、探索中に訪れた地点の情報を全て記憶しておく必要があるという点です。
たとえば、迷路を考えてみましょう。幅優先探索では、スタート地点から一歩進んだ場所、二歩進んだ場所…というように、順に探索範囲を広げていきます。この時、すでに通った道や行き止まりを覚えておかないと、同じ場所を何度も調べてしまったり、無限ループに陥ってしまう可能性があります。そのため、探索した場所の情報を全て記録しておく必要があるのです。
しかし、迷路が複雑になればなるほど、探索範囲が広がり、記録する情報量も膨大になります。これは、木の枝がどんどん増えていく様子に似ています。最初のうちは枝の数は少ないですが、枝分かれを繰り返すうちに、枝の数は爆発的に増加します。幅優先探索も同様に、探索の過程で記憶すべき情報量が急激に増え、コンピュータの記憶容量をすぐに超えてしまうかもしれません。
記憶容量を超えると、コンピュータは処理を続けられなくなり、探索が途中で止まってしまいます。これは、特に広大な迷路や分岐点の多い複雑な迷路で起こりやすい問題です。まるで、広大な図書館で目的の本を探すのに、調べた本棚の位置を全て覚えておく必要があるようなものです。調べた本棚が多すぎると、全てを覚えることは不可能になります。このように、幅優先探索は、記憶容量の限界という大きな壁に直面する可能性があるのです。
| 探索方法 | 説明 | メリット | デメリット | 例 |
|---|---|---|---|---|
| 幅優先探索 | 出発点から近い順に探索を行う。 | 最短経路を見つけられる。 | 探索した地点の情報を全て記憶する必要があるため、メモリ不足に陥る可能性がある。探索範囲が広がると、記憶すべき情報量が爆発的に増加する。 | 迷路、木の枝 |
他の探索方法

迷路を解くための道筋を見つける方法は、幅優先探索以外にもたくさんあります。それぞれの方法には得意な点や不得意な点があり、迷路の大きさや形、使える道具によって、どの方法を使うのが一番良いか決める必要があります。まずは深さ優先探索について説明します。この方法は、一本の道をできる限り深く進んでいく方法です。例えるなら、長い一本道を見つけたら、まずその道を最後まで進んでみるようなものです。もし行き止まりだったら、少し戻って別の道を進んでみます。この方法は、幅優先探索のように必ずしも一番短い道を見つけられるとは限りません。しかし、幅優先探索に比べて、記憶しておくべき情報が少ないため、使う道具が少ない状況でも役立ちます。
次に、もっと複雑な探索方法として、A*探索というものがあります。この方法は、ゴールまでの距離を予測しながら進むため、より効率的に最短経路を見つけ出すことができます。まるで、地図を見ながら、ゴールまでの距離を常に意識して進むようなものです。ただし、この方法は計算に時間がかかる場合もあります。
他にも、ランダムに道を選ぶ方法や、壁に沿って進む方法など、様々な探索方法があります。迷路が複雑で大きい場合、単純な探索方法では時間がかかりすぎたり、解を見つけられないこともあります。このような場合は、A*探索のような高度な方法を使うことで、より効率的に解を見つけることができます。しかし、高度な方法は複雑な計算が必要になるため、使える道具が多い場合にのみ有効です。
どの探索方法にも利点と欠点があり、迷路の規模や構造、そして利用可能な計算資源などを考慮して、最適な方法を選ぶ必要があります。例えば、小さな迷路であれば、単純な方法でも十分に解けますが、巨大で複雑な迷路では、より高度な方法が必要になります。また、使える道具が少ない場合は、記憶容量の少ない方法を選ぶ必要があります。
| 探索方法 | 説明 | 利点 | 欠点 | 適した状況 |
|---|---|---|---|---|
| 深さ優先探索 | 一本の道をできる限り深く進んでいく方法 | 記憶しておくべき情報が少ない | 必ずしも最短経路を見つけられるとは限らない | 使う道具が少ない状況 |
| 幅優先探索 | (本文に明示的な説明なし) | 最短経路を見つけられる | 記憶しておくべき情報が多い | (本文に明示的な記述なし) |
| A*探索 | ゴールまでの距離を予測しながら進む方法 | 効率的に最短経路を見つけ出すことができる | 計算に時間がかかる場合がある | 複雑な迷路、計算資源が豊富な場合 |
| ランダム探索 | ランダムに道を選ぶ方法 | (本文に明示的な記述なし) | (本文に明示的な記述なし) | (本文に明示的な記述なし) |
| 壁沿い探索 | 壁に沿って進む方法 | (本文に明示的な記述なし) | (本文に明示的な記述なし) | (本文に明示的な記述なし) |
まとめ

迷路を解く、つまり入り口から出口までの最短経路を見つける方法は、様々な場面で役立つ知識です。幅優先探索は、この問題を確実に解くことができる、強力な手法の一つです。
幅優先探索は、スタート地点から近い場所を、同心円状に広がるように探索していきます。まずスタート地点の隣接するマスを調べ、次にその隣接するマス、さらにその隣、というように探索範囲を広げていきます。まるで波紋が広がるように、段階的に探索していくのが特徴です。この手法を使うと、必ず最短経路を見つけることができます。なぜなら、より遠いマスを調べる前に、より近いマスを全て調べているからです。
しかし、幅優先探索には弱点もあります。それは、記憶しておくべき情報量が多いという点です。探索が進むにつれて、既に調べたマスを全て記憶しておく必要があり、迷路が大きくなると、必要な記憶容量も膨大になります。計算機の記憶領域を使い果たしてしまう可能性もあるため、大規模な迷路には適用しづらいという課題があります。
迷路探索は、計算機科学の基礎的な問題であり、幅優先探索以外にも、深さ優先探索など様々な手法があります。どの手法にも利点と欠点があり、状況に応じて適切な手法を選ぶ必要があります。例えば、記憶容量が限られている場合は、幅優先探索ではなく、別の探索方法を検討する必要があるでしょう。
様々な探索手法を理解し、使い分けることは、プログラムを作る上でも、様々な問題を解決する上でも、非常に大切です。今後、記憶容量の制約を克服し、より効率的に迷路を探索できる新しい手法が開発されることが期待されています。
| 項目 | 内容 |
|---|---|
| 手法 | 幅優先探索 |
| 目的 | 迷路の最短経路探索 |
| 探索方法 | スタート地点から同心円状に広がるように探索 |
| 利点 | 必ず最短経路を見つけられる |
| 欠点 | 記憶容量が大きい |
| 課題 | 大規模な迷路への適用が難しい |
| その他の手法 | 深さ優先探索など |
| 結論 | 状況に応じて適切な手法を選ぶ必要がある |
応用例

幅優先探索は、迷路の出口を見つけるといった単純な問題だけでなく、もっと複雑な課題を解決する際にも役立ちます。
例えば、インターネットのような巨大なネットワークを考えてみましょう。このネットワーク上では、データがどのように送受信されるかという経路を定める必要があります。このとき、最も効率的な経路を見つけ出すために、幅優先探索が用いられます。出発点から近い順に、次々に点を調べていくことで、最短の経路を見つけることができるのです。
また、パズルゲームを解く際にも、幅優先探索は力を発揮します。例えば、スライドパズルを考えてみましょう。バラバラになったピースを順番通りに並べ替えるためには、様々な手順を試す必要があります。このとき、幅優先探索を用いることで、無駄な手順を省き、最短の手順でパズルを解くことができるのです。
さらに、人工知能の分野でも、幅優先探索は重要な役割を担っています。人工知能では、コンピュータに人間のような知能を持たせることが目標とされています。そのためには、コンピュータに様々な状況を判断させ、適切な行動を選ばせる必要があります。この状況判断や行動選択を効率的に行うために、幅優先探索が利用されています。
このように、幅優先探索は情報技術の様々な分野で応用されています。インターネット、ゲーム、人工知能など、私たちの生活に欠かせない技術の裏側で、幅優先探索は静かに活躍しているのです。
| 分野 | 幅優先探索の活用例 |
|---|---|
| ネットワーク | インターネットにおけるデータ送受信の効率的な経路探索 |
| ゲーム | スライドパズルなどにおける最短手順の探索 |
| 人工知能 | 状況判断や行動選択の効率化 |
