幅優先探索で迷路を解く

AIを知りたい
先生、「幅優先探索」って、どういう意味ですか? 迷路を解くのに関係があるみたいですが、よくわかりません。

AIエンジニア
いい質問だね。幅優先探索は、迷路を解くための方法の一つだよ。スタート地点から、まずすぐ隣のマスを全部調べて、それからその隣のマス…というように、順番に調べていく方法なんだ。輪を描くように広がっていくイメージだよ。

AIを知りたい
なるほど。順番に調べていくんですね。でも、他の方法もあるんですか?

AIエンジニア
そうだよ。例えば、行き止まりまで進んでから戻る「深さ優先探索」っていう方法もある。幅優先探索は必ず最短ルートを見つけられるけど、たくさんの場所を覚えておかないといけないから、複雑な迷路だと大変なんだ。
幅優先探索とは。
人工知能に関係する言葉である「幅優先探索」について説明します。コンピューターで迷路を解くとき、まずスタート地点から順番に、あらゆる分かれ道を進んでいきます。そして、ゴール地点にたどり着く道筋が見つかれば、それが迷路の解となります。この探し方には、主に二つのやり方があり、探し方によってかかる時間に違いが出ます。「幅優先探索」では、スタート地点に近い点から順番に探していきます。そのため、ゴールまでの最短ルートを必ず見つけることができます。しかし、探している途中で立ち寄った点を全て記憶しておく必要があるため、複雑な迷路の場合、記憶容量が足りなくなってしまい、処理を続けられなくなることがあります。下のリンク先では、Pythonというプログラミング言語を使った「幅優先探索」のプログラムを実際に動かせる記事を公開しています。ぜひご覧ください。
幅優先探索とは

幅優先探索は、繋がりを持ったデータの集まり、例えば路線図や家系図のような構造の中で、ある地点から別の地点への道筋を見つけるための手順です。
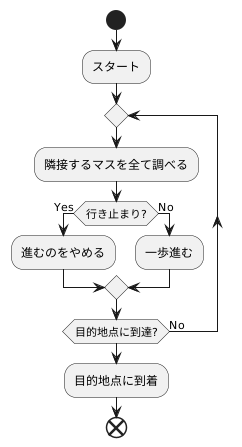
迷路を解くことを想像してみてください。あなたはスタート地点に立っています。まず、スタート地点に隣接する全てのマスを調べます。行き止まりなら、そこへは進めません。道が続いていたら、そこへ一歩進みます。次に、一歩進んだ地点からまた隣接する全てのマスを調べます。これを繰り返していくと、まるで水面に石を投げた時に波紋が広がるように、探索範囲がスタート地点を中心にして広がっていきます。これが幅優先探索です。
木の根元から枝が伸び、さらにその枝からまた枝が伸びていく様子を思い浮かべてください。幅優先探索は、根元から近い枝を先に探索し、徐々に遠い枝へと探索を広げていくイメージです。つまり、スタート地点に近い場所を優先的に調べるということです。
この手順の利点は、最初に見つかった道筋が、スタート地点から目的地点までの最短経路となることが保証されていることです。遠回りせずに、最も効率の良い道筋を見つけられるのです。
例えば、友達の友達の友達を辿って、世界中の人と繋がっていると言われています。幅優先探索を使えば、あなたと特定の人との間の最短の繋がりを見つけることができるでしょう。何人経由すればその人に辿り着けるのか、最短ルートで知ることができるのです。
探索の仕組み

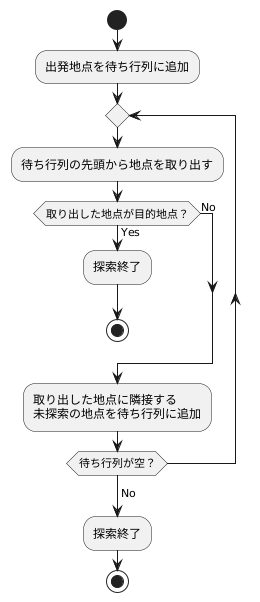
探索とは、ある地点から目的の地点までの道筋を見つけることです。様々な方法がありますが、ここでは「幅優先探索」と呼ばれる方法について詳しく説明します。
幅優先探索は、「待ち行列」と呼ばれるデータ構造を使って行います。この待ち行列は、「先に入れたものを先に出す」という規則で、これから探索する地点を記憶しておくためのものです。
まず、出発地点を待ち行列に入れます。次に、待ち行列から一番先に入っている地点を取り出します。そして、その地点に隣接している、まだ探索していない地点を全て待ち行列に追加します。
この地点の追加は、隣接する地点が複数ある場合、全て一度に待ち行列の後ろに追加されます。例えば、東、西、北の3つの地点が隣接している場合、これら3つを待ち行列に追加します。
その後、再び待ち行列から一番先に入っている地点を取り出し、同様に隣接する未探索の地点を待ち行列に追加します。これを繰り返すことで、出発地点に近い地点から順に、徐々に探索範囲を広げていくことができます。
まるで、池に石を投げ入れた時に、波紋が円状に広がっていく様子を想像してみてください。石を投げ入れた場所が出発地点で、波紋が広がるように探索範囲が徐々に広がっていきます。
探索済みの地点は記録しておき、同じ地点を何度も探索しないようにすることで、無駄を省き、効率的に目的の地点を探し出すことができます。目的の地点が見つかった場合、もしくは探索する地点がなくなってしまった場合は、探索を終了します。
最短経路の保証

幅優先探索は、目的地点までの最短経路を見つけることが保証されている、大変便利な探索手法です。この手法は、出発地点から近い場所を、波紋のように順々に広げていくイメージで探索を行います。まず、出発地点に隣接する場所を全て調べます。次に、それらの場所に隣接する、まだ調べていない場所を調べます。これを繰り返すことで、目的地点にたどり着くまで探索範囲を広げていきます。
この探索方法の利点は、目的地点に初めて到達したとき、その経路が必ず最短経路になることです。なぜなら、近い場所から順に調べているため、より短い経路があれば、そちらを先に発見するからです。例えば、出発地点から目的地点まで3つの経路があるとします。一つは3歩、もう一つは5歩、最後は7歩の経路です。幅優先探索では、まず出発地点の周りの1歩先の場所を全て調べ、次に2歩先の場所、そして3歩先の場所を調べます。3歩先の場所に目的地点があれば、そこで探索は終了です。5歩や7歩の経路を調べる前に、最短の3歩の経路を見つけることができます。
他の探索方法では、必ずしも最短経路を見つけられるとは限りません。例えば、深さ優先探索という方法は、一つの道を可能な限り深く掘り下げて探索します。行き止まりにぶつかったら、一つ前の分岐点に戻り、別の道を深く探索します。この方法では、たまたま最初に長い経路を見つけてしまう可能性があります。目的地点に到達しても、それが最短経路かどうかは分かりません。他の経路を全て探索し終えるまで、最短経路は確定しません。
このように、最短経路を見つけられるという点で、幅優先探索は他の探索方法に比べて大きな利点を持っていると言えます。確実に最短経路を見つけたい場合は、幅優先探索を使うのが賢明です。
| 探索手法 | 説明 | 最短経路 |
|---|---|---|
| 幅優先探索 | 出発地点から近い場所を波紋のように広げていくように探索。 | 保証されている |
| 深さ優先探索 | 一つの道を可能な限り深く掘り下げて探索し、行き止まりにぶつかったら一つ前の分岐点に戻って別の道を探索。 | 保証されていない |
メモリの使用量

幅優先探索は、迷路や複雑な繋がりを調べる際に、既に調べた場所を全て覚えておく必要があります。このため、複雑な迷路や繋がりを多く持つ図形では、記憶しておくべき情報が増え、装置の記憶容量を多く使うことになります。
探索を進めるにつれて、次に調べる場所の順番を記録するリストも長くなり、最悪の場合、装置の記憶容量が足りなくなることもあります。特に、探索範囲が広かったり、分岐点が多い迷路や図形では、記憶容量の使用量に気を配る必要があります。
例えば、大きな地図で道を探す場面を想像してみてください。出発地点から近い場所を順番に調べていくと、既に調べた場所を覚えておく必要があります。そうでなければ、同じ場所を何度も調べてしまったり、目的地にたどり着くための最短経路を見つけることが難しくなります。
このとき、調べた場所を全て地図に書き込んでいくと、地図がどんどん複雑になり、見づらくなってしまいます。同様に、装置の中で記憶しておく情報が増えすぎると、処理速度が遅くなったり、最悪の場合、装置が停止してしまう可能性もあります。
そのため、非常に大きなデータや複雑な繋がりを扱う場合は、記憶容量を効率的に使える方法を考える必要があります。例えば、既に調べた場所の情報の一部を消去したり、必要な情報だけを記憶するように工夫することで、記憶容量の不足を防ぐことができます。状況に応じて、記憶容量の使い方を工夫することで、より効率的な探索を行うことが可能になります。
| 問題点 | 具体例 | 対策 |
|---|---|---|
| 探索済み場所の記憶増加 | 複雑な迷路、多接続図形 | 記憶容量の効率化 |
| 探索リストの肥大化 | 広範囲探索、分岐点多数 | 記憶容量の効率化 |
| 記憶容量不足 | 大きな地図での経路探索 | 不要情報消去、必要情報のみ記憶 |
| 処理速度低下、装置停止 | 大規模データ、複雑な繋がり | 状況に応じた記憶容量管理 |
適用事例

幅優先探索は、様々な場面で活用されている、汎用性の高い手法です。身近な例では、カーナビゲーションシステムでの経路探索があります。出発地から目的地までの最適な経路を見つける際に、幅優先探索は有効です。交差点を分岐点として捉え、出発地から近い順に全ての経路を探索することで、最短経路を見つけ出します。
また、ネットワークにおいても、幅広い活用が見られます。例えば、インターネット網におけるデータの転送経路の決定に、幅優先探索が利用されています。送信元から受信先までの最適な経路を探索することで、データ転送の効率化を図ることができます。複数の経路候補の中から、通信速度や安定性などを考慮し、最適な経路を選択することが可能です。
さらに、パズルゲームの解法にも、幅優先探索は応用できます。例えば、迷路の最短経路を見つける問題や、数当てゲームの解答を導き出す問題など、様々なパズルゲームにおいて、幅優先探索は強力なツールとなります。初期状態から可能な状態を順次探索していくことで、解に辿り着くまでの手順を明らかにすることができます。
人工知能の分野でも、幅優先探索は重要な役割を担っています。例えば、ゲームにおける人工知能の思考アルゴリズムに、幅優先探索が利用されることがあります。可能な手を全て探索し、勝利につながる最適な手を選択することで、人工知能は高度な戦略を立てることができます。
このように、幅優先探索は、経路探索、ネットワーク解析、パズルゲーム、人工知能など、様々な分野で活用されている、非常に汎用性の高いアルゴリズムです。問題解決のための強力なツールとして、幅広い応用範囲を持っています。
| 分野 | 活用例 |
|---|---|
| 経路探索 | カーナビゲーションシステムでの最適経路探索 |
| ネットワーク | インターネット網におけるデータ転送経路の決定 |
| パズルゲーム | 迷路の最短経路探索、数当てゲームの解答導出 |
| 人工知能 | ゲームにおけるAIの思考アルゴリズム |
実装例

幅優先探索は、様々なプログラムを組む言葉で比較的簡単に実現できます。特に、Pythonのような手軽に使える言葉では、リストや待ち行列といったデータ構造を使うことで、簡潔に表現できます。インターネット上には、公開されている例文のプログラムもたくさんあります。そのため、実際に動かしてその動きを確かめることも容易です。仕組みを深く理解するためには、実際にプログラムを書いて、動かしてみることをお勧めします。
例えば、迷路を解く場面を考えてみましょう。幅優先探索は、スタート地点から近い場所を順に調べていく方法です。まず、スタート地点を待ち行列に入れます。次に、待ち行列から最初の地点を取り出し、その隣のまだ調べていない地点を待ち行列に追加します。この時、追加した地点がゴール地点であれば探索終了です。ゴール地点でなければ、さらに待ち行列から地点を取り出し、その隣の地点を調べます。これを繰り返すことで、スタート地点から近い順に全ての地点を調べることができます。まるで、波紋が広がるように探索範囲が広がっていく様子を想像してみてください。
Pythonでこの探索方法を実現する場合、リストを待ち行列として使うことができます。リストの先頭に地点を追加し、末尾から地点を取り出す操作を繰り返すことで、幅優先探索を実現できます。また、既に調べた地点を記録するためのリストも用意しておくと、同じ地点を何度も調べずに済みます。
Pythonを使った幅優先探索の実装例は、インターネットで検索するとたくさん見つかります。様々な例を参考にしながら、実際にプログラムを書いて、迷路の探索や、友達関係のネットワーク分析など、身近な問題を解いてみましょう。そうすることで、幅優先探索の仕組みをより深く理解し、応用力を高めることができます。
