特異値分解:行列の本質を見抜く

AIを知りたい
先生、「特異値分解」って難しそうだけど、何のために使うんですか?行列を分解するっていうのはなんとなくわかるんですけど…

AIエンジニア
そうだね、難しそうに見えるけど、使い道はたくさんあるよ。例えば、画像データからノイズを取り除いたり、データの重要な特徴を掴んで圧縮したりするのに使われるんだ。分解することで、データの本質的な情報だけを取り出すことができるんだよ。

AIを知りたい
なるほど。でも、どうやって本質的な情報だけを取り出すことができるんですか?

AIエンジニア
特異値分解では、分解した結果の対角行列Σの中に「特異値」と呼ばれる値が入っているんだ。この特異値の大きさが、データの重要度を表していて、小さい特異値に対応する情報はノイズとして扱って捨ててしまうことで、本質的な情報だけを残すことができるんだよ。
特異値分解とは。
人工知能の分野でよく使われる「特異値分解」という用語について説明します。特異値分解とは、どんな行列でも、三つの行列の掛け算に変換する手法のことです。掛け合わせる三つの行列は、それぞれ特別な性質を持っています。一つ目は「直交行列U」、二つ目は「対角行列Σ」、三つ目は「直交行列Vの転置行列(V*)」です。この変換を使うことで、行列の中で重要な情報だけを取り出すことができます。
特異値分解とは

どんな形をしている行列でも、もっと簡単な形に変換できる強力な方法があります。それが特異値分解です。この方法を使うと、どんな行列も三つの特別な行列の積に変換できます。
一つ目は直交行列と呼ばれる行列で、これは二回出てきます。直交行列は、それぞれの列の向きが互いに直角になっており、かつ、それぞれの列の長さが全て1になっているという特別な行列です。
二つ目は対角行列と呼ばれる行列で、これは成分が対角線上にしか存在しない行列です。対角線以外の場所の成分は全てゼロになっています。
この三つの行列のかけ算で、元の行列を表現することができます。数式で書くと「UΣV*」のようになります。ここで、UとVは直交行列、Σは対角行列、V*はVの転置共役行列を表します。転置共役行列とは、行列の行と列を入れ替えて、さらに各成分を複素共役にした行列です。実数の行列の場合は、単に行と列を入れ替えた転置行列と同じになります。
このように、行列を直交行列と対角行列に分解することを特異値分解といいます。特異値分解によって、一見複雑に見える行列も、その本質を明らかにすることができます。具体的には、Σの対角成分である特異値を見ることで、元の行列の重要な情報を得ることができます。大きな特異値に対応する部分は、元の行列の中で重要な役割を果たしていることを示しています。逆に、小さな特異値に対応する部分は、元の行列の情報にあまり影響を与えていないことを示しています。
この性質を利用することで、画像の圧縮やノイズ除去、データの次元削減など、様々な分野に応用されています。例えば、画像を特異値分解し、小さな特異値を無視することで、データ量を削減しながら画像の重要な特徴を保持することができます。
分解の仕組み

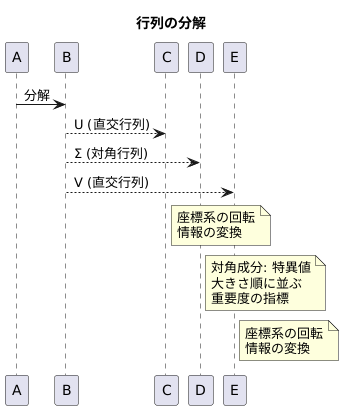
分解の仕組みについて詳しく説明します。分解とは、ある行列を三つの行列の積の形に変換する操作のことを指します。この操作を行うことで、元の行列が持つ情報を整理し、重要な要素を抜き出すことができます。
三つの行列のうち、二つは直交行列と呼ばれ、それぞれUとVという記号で表されます。直交行列は、座標系の回転のような役割を果たします。つまり、UとVは、元の行列が持つ情報を、より分かりやすい座標系に変換する働きをしています。
もう一つの行列は、対角行列と呼ばれ、Σという記号で表されます。対角行列とは、対角線上の成分以外はすべてゼロであるような行列のことです。この対角行列Σの対角線上の成分は、特異値と呼ばれています。特異値は、元の行列の重要な情報を担っており、その大きさによって重要度が分かります。特異値は、大きさの順に並んでいます。
この特異値の大きさを見ることで、どの情報が重要なのかを判断することができます。大きな特異値に対応する情報は重要であり、小さな特異値に対応する情報は重要度が低いと判断できます。小さな特異値は、元の行列の情報の中で重要度の低い部分を担っているため、これらを切り捨てることで、データの次元を削減することができます。次元を削減するということは、扱うデータの量を減らすということであり、処理の効率化につながります。例えば、画像データの圧縮などに利用されています。多くの画像データは、実際には必要のない情報も多く含まれています。分解を用いることで、重要な情報だけを残し、不要な情報を捨てることで、データ量を減らし、効率的に保存したり、処理したりすることができるようになります。
重要な情報の抽出

特異値分解は、膨大な情報の海から宝物を探し出すような手法です。まるで砂金採りのように、大量の砂の中から金だけを抽出するように、データに含まれる重要な情報だけを抜き出すことができます。この手法の肝となるのが、特異値と呼ばれる数値です。
特異値分解を行うと、データはいくつかの特異値とそれに対応する情報に分解されます。重要なのは、これらの特異値は大きさの順に並んでいるという点です。大きな特異値に対応する情報は、データの中で中心的な役割を果たす重要な部分であり、逆に小さな特異値に対応する情報は、さほど重要でない細かな部分や雑音に過ぎません。
例えば、一枚の写真を考えてみましょう。この写真を特異値分解すると、大きな特異値に対応する情報は、写真の主要な構成要素、例えば人物の輪郭や背景の建物といった全体像を捉える情報になります。一方、小さな特異値に対応する情報は、写真の細かい部分、例えば肌の質感の微妙な変化や背景の些細な模様といった、全体像への影響が少ない情報になります。
この性質を利用することで、小さい特異値とそれに対応する情報を無視することで、データの主要な特徴だけを残し、不要な情報を削除することができます。写真で言えば、小さな特異値を無視することは、写真のノイズを取り除き、主要な被写体や背景をはっきりとさせることに相当します。これは、データの容量を削減するデータ圧縮や、ノイズを除去してデータの本質を捉えるノイズ除去に非常に役立ちます。このように、特異値分解は、データの本質を見抜くための強力な道具と言えるでしょう。
| 概念 | 説明 | 写真での例 |
|---|---|---|
| 特異値分解 | データから重要な情報(特異値)を抽出する手法 | 写真から主要な構成要素を抽出 |
| 大きな特異値 | データの中心的な役割を果たす重要な情報 | 人物の輪郭、背景の建物など |
| 小さな特異値 | 重要でない細かな部分やノイズ | 肌の質感、背景の些細な模様など |
| 特異値分解の応用 | データ圧縮、ノイズ除去 | ノイズ除去、主要被写体や背景の強調 |
次元削減への応用

多くの情報を持つデータは、たくさんの要素で表現されることがよくあります。例えば、たくさんの数字の列で表されるようなものを高次元データと言います。このようなデータは、扱うのが大変で、計算に時間がかかったり、全体像を掴むのが難しかったりします。そこで、データの持つ大切な特徴はそのままに、表現する要素の数を減らす方法が重要になります。これを次元削減と言います。
特異値分解はこの次元削減で活躍します。特異値分解は、複雑な行列を、より単純な行列の積に分解する方法です。この分解によって、データの中に隠れている重要な情報が、特異値と呼ばれる値の大きさで分かります。大きな特異値に対応する情報は重要で、小さな特異値に対応する情報はあまり重要ではありません。そこで、小さな特異値とそれに対応する情報を無視することで、データの持つ重要な特徴はなるべく残したまま、表現する要素の数を減らすことができます。
例えるなら、たくさんの色鉛筆で描かれた絵があるとします。よく見ると、使われている色のほとんどは、数色の組み合わせで表現できることに気付くかもしれません。特異値分解は、この絵の中で主要な色の役割をする重要な要素を見つけ出し、あまり使われていない細かい色の情報を省略するような働きをします。結果として、使う色鉛筆の本数は減りますが、絵の全体的な印象は大きく変わりません。
このようにして次元削減されたデータは、元のデータと比べて計算処理の負担が軽くなり、データの全体像を掴みやすくなります。このため、機械学習やデータの分析など、様々な分野で広く使われています。例えば、大量の文章データを分析する場合や、顔認識技術で顔の特徴を捉える場合など、次元削減はデータ処理を効率化する上で欠かせない技術となっています。
| 項目 | 説明 |
|---|---|
| 高次元データ | 多くの要素で表現されるデータ(例:多数の数字列) |
| 次元削減 | データの重要な特徴を維持しつつ、表現する要素の数を減らす方法 |
| 特異値分解 (SVD) | 複雑な行列を単純な行列の積に分解する次元削減手法。重要な情報は大きな特異値に対応。 |
| 特異値の役割 | データの重要度を示す指標。大きな特異値は重要な情報、小さな特異値は重要でない情報を表す。 |
| 次元削減の効果 | 計算処理の負担軽減、データ全体像の把握の容易化 |
| 応用例 | 機械学習、データ分析(例:大量の文章データ分析、顔認識) |
推薦システムでの活用

特異値分解は、様々な分野で活用されていますが、特にインターネット上のサービスでよく見かける商品の推薦システムにも役立っています。この推薦システムは、利用者の過去の行動や評価を基におすすめの商品を提示する仕組みです。
具体的には、利用者の購買履歴や商品への評価などを数値で表し、それを大きな表にまとめます。この表は行に利用者、列に商品が並び、それぞれの交わるマスには評価や購入回数などの情報が入ります。特異値分解はこのような大きな表を分析するのに非常に適しています。
特異値分解を行うことで、この大きな表に隠された重要な情報を取り出すことができます。例えば、ある利用者が特定の種類の商品をよく購入している場合、その利用者はその種類の商品を好む傾向があると判断できます。また、複数の利用者から高い評価を受けている商品は、品質が高い、もしくは多くの人に好まれる特徴を持っていると推測できます。特異値分解は、このような傾向や特徴を数値として捉え、利用者の好みや商品の特性を抽出することを可能にします。
特異値分解を用いた推薦システムは、利用者がまだ知らない商品との出会いを提供します。例えば、ある利用者が特定のジャンルの映画をよく見ているとします。特異値分解は、その利用者の好みに基づいて、まだ見ていない同じジャンルの映画や、似たような雰囲気の映画を推薦することができます。また、多くの利用者から高評価を受けている人気の商品を推薦することも可能です。このように、特異値分解は、利用者の行動履歴や評価だけでなく、他の利用者の評価も加味して、より精度の高い、個人に最適化された商品推薦を実現しています。
現在、多くの買い物サイトや動画配信サービスなどで、この特異値分解を用いた推薦システムが利用されており、利用者の満足度向上に大きく貢献しています。今まで知らなかった商品との出会い、自分の好みにぴったりの商品との出会いは、利用者にとって大きな喜びとなるでしょう。特異値分解は、このようなインターネット上のサービスをより便利で快適なものにするために、重要な役割を担っていると言えるでしょう。
| 項目 | 説明 |
|---|---|
| 特異値分解の活用例 | インターネット上の商品の推薦システム |
| 推薦システムの仕組み | 利用者の過去の行動や評価を基におすすめの商品を提示 |
| データの表現方法 | 利用者を行、商品を列とする表に評価や購入回数などの情報を格納 |
| 特異値分解の役割 | 大きな表に隠された重要な情報(利用者の好みや商品の特性)を抽出 |
| 特異値分解による利点 | 利用者がまだ知らない商品との出会いを提供、好みに最適化された商品推薦 |
| 適用例 | 買い物サイト、動画配信サービスなど |
| 効果 | 利用者の満足度向上 |
画像処理への応用

写真は、小さな点の集まりでできています。一つ一つの点の明るさを数字で表し、それを縦横に並べたものが行列です。この行列を特異値分解という方法で解析することで、写真の様々な処理を行うことができます。
特異値分解とは、行列をいくつかの特別な行列の積に分解する手法です。分解された行列は、元の行列の重要な特徴を表しています。写真に置き換えて考えると、これらの行列は写真の主要な情報を抽出したものと言えます。
例えば、人の顔を認識するシステムを考えてみましょう。顔写真から目や鼻、口といった重要な特徴を捉える必要があります。特異値分解を使うと、顔写真からこれらの特徴を数値として抽出できます。この数値を基に、コンピュータは様々な顔を見分けることができるようになります。
また、写真には不要なノイズが含まれる場合もあります。これは、写真の質を落とす原因となります。特異値分解は、このノイズを取り除くのにも役立ちます。分解された行列の中から、ノイズに相当する部分を特定し、その影響を取り除くことで、より鮮明な写真を得ることができます。
医療現場で使われる写真でも、特異値分解は活躍しています。レントゲン写真やMRI画像などから、病気の兆候を見つけやすくするために、ノイズ除去や画像の鮮明化が行われます。特異値分解は、医療診断の精度向上に貢献している重要な技術と言えるでしょう。
このように、特異値分解は写真の情報を解析し、様々な処理を行うための強力な道具です。様々な分野で活用されており、今後もその応用範囲は広がっていくと考えられます。
| 分野 | 特異値分解の用途 | 効果 |
|---|---|---|
| 顔認識システム | 顔写真から目、鼻、口などの特徴を数値として抽出 | 様々な顔を見分けることが可能 |
| 写真全般 | ノイズの除去 | 鮮明な写真を得ることが可能 |
| 医療現場 | レントゲン写真やMRI画像のノイズ除去、鮮明化 | 医療診断の精度向上 |
