探索木:コンピュータの迷路攻略法

AIを知りたい
先生、『探索木』って、どういうものですか? 迷路を解くのに使うって聞いたんですけど、木とは何かイメージがわきません。

AIエンジニア
そうだね、木のような構造をしているから、探索木と呼ぶんだよ。迷路の入口から、それぞれの分かれ道を枝分かれのように記録していくんだ。それぞれの分かれ道が枝のように伸びて、全体としては木のような形になるんだよ。

AIを知りたい
なるほど。じゃあ、もし行き止まりだったらどうするんですか?

AIエンジニア
行き止まりにたどり着いたら、一つ前の分かれ道まで戻って、まだ進んでいない道を選ぶんだ。これを繰り返していくことで、すべての道を探索できる。木で例えると、枝の先まで行って行き止まりだったら、一つ手前の枝に戻って別の枝を進むイメージだね。
探索木とは。
コンピュータで迷路を解くときなどに使う、木のような構造のことを『探索木』と言います。
探索木とは

探索木とは、データを木構造と呼ばれる、階層的な繋がりを持つ形で整理し、効率的に探索を行うための手法です。木構造は、根と呼ばれる出発点から、枝分かれのようにデータが繋がっています。ちょうど、植物の根から茎、そして枝や葉が広がる様子に似ています。
この木構造を用いることで、データの検索、挿入、削除といった操作を効率的に行うことができます。例えば、電話番号帳から特定の人の番号を探す場面を想像してみてください。五十音順に並べられた膨大な数の名前の中から、目的の名前を探すのは大変な作業です。しかし、もし名前が木構造で整理されていれば、五十音順の最初の文字でグループ分けされ、さらに次の文字、その次の文字と、段階的に絞り込んでいくことで、目的の名前を素早く見つけることができます。
探索木における各データは、節点と呼ばれます。そして、各節点には、それよりも小さな値を持つ子節点と、大きな値を持つ子節点が存在します。これを左右の子節点と呼ぶこともあります。根となる節点は、他のどの節点よりも大きな値、もしくは小さな値を持ちます。新しいデータを挿入する際には、根から出発し、挿入するデータの値と各節点の値を比較しながら、適切な場所に配置します。小さい値であれば左へ、大きい値であれば右へ進んでいくことで、常に大小関係が保たれた状態を維持します。
このように、探索木はデータの整理と探索を効率化するための優れた仕組みです。大量のデータを扱う場面で、その真価を発揮します。例えば、データベース検索、経路探索、人工知能など、様々な分野で応用されています。まるで、複雑な迷路を解くための地図のように、膨大な情報の中から必要な情報へ素早くアクセスするための道筋を示してくれるのです。
迷路攻略における役割

道に迷った時、どのようにして出口を探しますか? 行き止まりまで進んで戻ったり、分かれ道でどちらの道を選ぶか悩んだりするでしょう。このような状況を整理し、効率的に解決するために役立つのが「探索木」という考え方です。
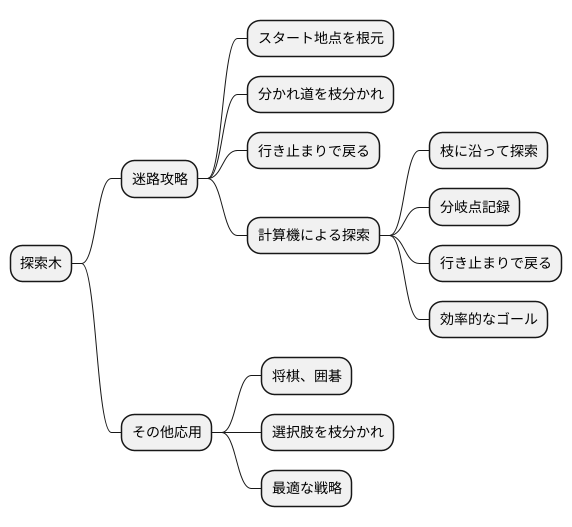
迷路を解く場面を想像してみてください。スタート地点を木の根元とします。そこから伸びる道は木の枝のように、分かれ道ごとに枝分かれしていきます。例えば、最初の分かれ道で右と左の道があれば、根元から右と左に枝が伸びます。さらにそれぞれの道が分岐すれば、そこからまた枝が伸びていきます。このように、迷路の構造全体を木の形に表すことで、道筋を視覚的に把握できるようになります。
この木構造は、計算機にとっても迷路を解くための強力な道具となります。計算機は、木の枝に沿って一つずつ道筋をたどることができます。分かれ道に到達するたびに、どの枝を進んだかを記録し、行き止まりにぶつかった場合は、一つ前の分岐点まで戻って別の枝を進みます。この動作は、まるで毛糸玉を巻き戻しながら、来た道を戻るようなものです。どの道を通ったか、どこで行き止まりになったかを記録することで、同じ道を何度も通る無駄を省き、効率的にゴールを目指せるのです。
探索木は、迷路攻略だけでなく、様々な問題解決に応用できます。例えば、将棋や囲碁などのゲームで、次にどの手を打つべきかを考える場合にも、この木構造を利用することができます。様々な選択肢を枝分かれのように広げ、どの選択肢が最良の結果に繋がるかを探索することで、最適な戦略を見つけることができるのです。
木の構造

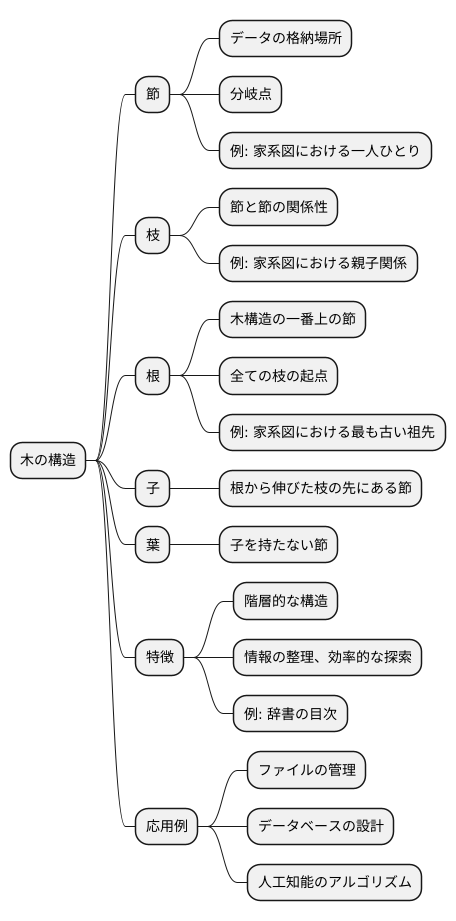
木の構造とは、まさに植物の木のような形をしたデータの繋がり方を指します。節と枝が組み合わさり、階層的な構造を作り上げています。この構造は、まるで根っこから幹が伸び、そこから枝が分かれ、さらに小さな枝が生えていく様子とよく似ています。
木の構造で最も基本となるのは「節」です。節は、データの格納場所であり、木構造における各々の分岐点を表します。例えば、家系図を思い浮かべてみると、一人ひとりの人が節にあたります。そして、節と節の間を繋ぐのが「枝」です。枝は、節同士の関係性を示しています。家系図で言えば、親子関係が枝で表現されます。
木構造の一番上の節を「根」と呼びます。根は、木の始まりであり、全ての枝はこの根から伸びています。家系図でいえば、最も古い祖先が根にあたります。根から伸びた枝の先にある節を「子」と呼び、子からさらに枝が伸び、その先にまた節ができます。これを繰り返すことで、木はどんどん大きく成長していきます。また、子を持たない節を「葉」と呼びます。
木構造は、情報を整理し、効率的に探索するための優れた方法です。例えば、辞書の語を探す場合、最初から順番に見ていくよりも、目次を活用して目的のページに近い場所を開く方がはるかに速く見つけることができます。これは、辞書の目次が木構造のような階層構造になっているためです。木構造を使うことで、膨大なデータの中から必要な情報を素早く探し出すことができるのです。
このように、木構造はデータの繋がり方を視覚的に分かりやすく表現し、効率的な探索を可能にすることから、様々な場面で活用されています。例えば、ファイルの管理、データベースの設計、人工知能のアルゴリズムなど、幅広い分野で応用されています。
探索木の活用例

探索木は、項目を探したり、整理したり、最適な手順を見つけるための基本的な道具です。まるで樹木の枝のようにデータが繋がり、根から枝の先へ辿ることで目的の情報にたどり着けます。この構造は、様々な場面で役に立っています。
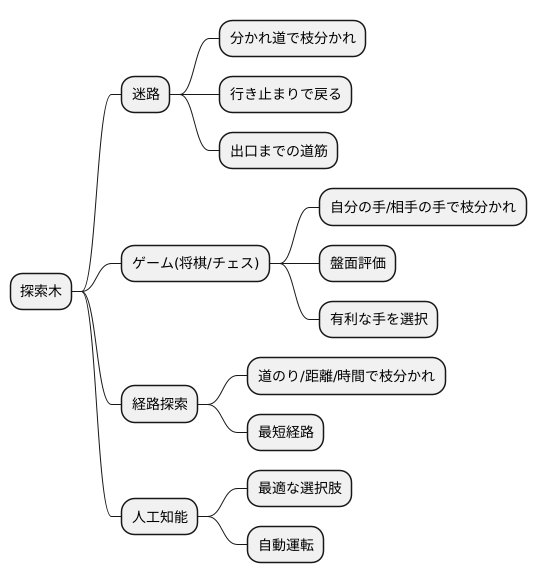
例えば、迷路を解くことを考えてみましょう。迷路の分かれ道ごとに、どの道を選ぶかを枝分かれのように表せます。行き止まりに突き当たったら、一つ前の分かれ道に戻り、別の道を選びます。このように、探索木を使って全ての道を探索し、出口までの道筋を見つけることができます。
また、将棋やチェスのようなゲームでも探索木は力を発揮します。自分の指せる手を枝分かれのように広げ、相手の手も同様に枝分かれさせていきます。すると、これから起こりうる盤面が木の枝のように広がっていきます。それぞれの盤面で、駒の配置や戦況から有利不利を判断し、最も有利になる手を選ぶことで、勝利に近づくことができます。
目的地までの最適な経路を見つける場合にも探索木は役立ちます。出発地から目的地までの道のりを枝分かれで表し、それぞれの道の距離や所要時間などの情報を加えます。すると、最も短い距離や最短時間で到着できる経路を簡単に見つけることができます。
さらに、人工知能の分野でも探索木は広く使われています。膨大な数の選択肢から最適なものを選ぶ必要がある場合、全ての選択肢を一つずつ調べるのは大変な作業です。探索木を使うことで、効率的に最適な選択肢を見つけ出すことができます。例えば、自動運転技術では、周囲の状況を把握し、安全かつスムーズな走行経路を計算するために探索木が活用されています。このように、探索木は複雑な問題を解決するための重要な道具となっています。
探索方法の種類

様々な種類がある探索木を使った探索方法の中で、代表的な二つの方法を詳しく見ていきましょう。一つ目は幅優先探索です。これは、木の根元、つまり出発点から近い場所を優先的に調べていく方法です。迷路を探索するときを想像してみてください。スタート地点からすぐ近くの道を全て調べて、そこからまた一歩ずつ、周りの道を調べていく方法が幅優先探索です。この方法を使うと、出発点から最短距離で見つかる解を確実に見つけることができます。例えば、スタート地点から一番近い場所に宝がある場合、幅優先探索を使えば最短の手数で宝を見つけることができます。しかし、探索する木の枝が広範囲に広がっている場合、多くの記憶領域が必要になるという欠点もあります。
二つ目は深さ優先探索です。これは、幅優先探索とは異なり、一つの道を可能な限り深く進んでから、次の道を探し始める方法です。迷路で考えると、一本の道を突き進んで行き止まりにぶつかってから、分岐点まで戻り、別の道を進んでいくイメージです。この方法は、幅優先探索に比べて記憶領域が少なくて済むという利点があります。なぜなら、一度探索した道は記憶しておく必要がなく、現在進んでいる道とその分岐点の情報だけを覚えていれば良いからです。しかし、探索する木が非常に深い場合、探索に時間がかかったり、目的の解にたどり着けない可能性もあります。また、見つかった解が必ずしも最短距離の解ではないという点にも注意が必要です。このように、幅優先探索と深さ優先探索はそれぞれ異なる特徴を持っています。そのため、解決しようとする問題の性質や探索木の構造を理解し、どちらの方法がより適しているかを判断することが重要です。
| 探索方法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 幅優先探索 | 出発点から近い場所を優先的に調べていく方法。迷路では、スタート地点からすぐ近くの道を全て調べて、そこから一歩ずつ周りの道を調べていくイメージ。 | 出発点から最短距離で見つかる解を確実に見つけることができる。 | 探索する木の枝が広範囲に広がっている場合、多くの記憶領域が必要になる。 |
| 深さ優先探索 | 一つの道を可能な限り深く進んでから、次の道を探し始める方法。迷路では、一本の道を突き進んで行き止まりにぶつかってから、分岐点まで戻り、別の道を進んでいくイメージ。 | 幅優先探索に比べて記憶領域が少なくて済む。 | 探索する木が非常に深い場合、探索に時間がかかったり、目的の解にたどり着けない可能性もある。見つかった解が必ずしも最短距離の解ではない。 |
利点と欠点

探索木は、様々な問題を解くための強力な道具であり、長所と短所を併せ持っています。まず、探索木を使うことの大きな利点は、問題を整理して捉えることができる点です。複雑に絡み合った問題も、木構造を使うことで、幹から枝葉へと広がる視覚的に分かりやすい形に整理できます。まるで地図のように、問題の全体像と個々の要素の関係性を把握できるため、解決策を見つけるための道筋が立てやすくなります。また、探索木には、効率的な探索方法がたくさん考案されていることも利点です。これらの方法は、先人たちの知恵が詰まった、いわば「近道」のようなものです。これらの近道を使うことで、全ての枝葉を一つ一つ調べることなく、目的の場所に素早くたどり着くことができます。例えば、迷路を解くとき、行き止まりまで進んでから引き返すよりも、より効率的な方法があるように、探索木にも無駄を省いた探索方法が存在します。
一方で、探索木には規模が大きくなりすぎるという欠点もあります。選択肢が多い問題では、枝分かれの数が増え続け、まるで雪だるま式に膨らむ風船のように、探索木の規模が爆発的に増大してしまうことがあります。これは、計算を行う装置にとって大きな負担となり、膨大な時間と資源が必要になる可能性があります。例えば、将棋や囲碁のように、一手ごとに無数の手が生じるような複雑なゲームでは、全ての可能性を網羅しようとすると、途方もない量の計算が必要になります。このような場合には、探索木の規模を小さく抑える工夫が重要になります。不要な枝葉を剪定するように、探索範囲を絞り込むことで、効率的な探索を実現できます。また、問題の特徴を良く理解し、その性質に合った探索木の手法を選ぶことも重要です。ちょうど、高い山に登るのに適した装備があるように、問題の種類に応じて適切な道具を選ぶことで、探索をスムーズに進めることができます。このように、探索木は、その利点と欠点を理解し、適切に活用することで、複雑な問題解決に役立つ強力な道具となります。
| 項目 | 内容 |
|---|---|
| 長所 | 問題を整理して捉えることができる 効率的な探索方法が多数存在する |
| 短所 | 規模が大きくなりすぎる可能性がある |
| 長所詳細 | 木構造により問題の全体像と個々の要素の関係性を把握しやすく、解決策の道筋を立てやすい 先人の知恵が詰まった効率的な探索方法(近道)により、目的の場所に素早くたどり着ける |
| 短所詳細 | 選択肢が多い問題では、枝分かれの数が増え続け、探索木の規模が爆発的に増大する 膨大な時間と資源が必要になる可能性がある 例:将棋、囲碁など |
| 対策 | 探索木の規模を小さく抑える工夫 探索範囲を絞り込む 問題の特徴に合った探索木の手法を選ぶ |
