クイックソート徹底解説

AIを知りたい
先生、クイックソートって基準値より大きいか小さいかで分けるってどういうことですか?

AIエンジニア
そうだね。例えば、数字の列を小さい順に並べ替える場合を考えてみよう。まず、列の中から適当に基準となる数字を選びます。そして、その基準値より小さい数字を左側に、大きい数字を右側に移動させるんだ。

AIを知りたい
基準値で左右に分けた後はどうするんですか?

AIエンジニア
分けた左側と右側のグループそれぞれで、また同じように基準値を決めて、大小で分ける操作を繰り返すんだ。これを繰り返していくと、最終的に全体が小さい順に並び変わっているんだよ。
クイックソートとは。
ある値を基準にして、それよりも大きいか小さいかで分けていくことで、最終的に全体を順番通りに並べ替える方法。この方法は『クイックソート』と呼ばれ、人工知能の分野でよく使われる言葉です。
クイックソートとは

クイックソートとは、多くの種類がある並び替え方法の中でも特に速いことで知られる方法です。この方法は、まるで整理整頓が得意な人が、たくさんの物をグループ分けして、さらに小さなグループに分けていくように、巧みにデータの並び替えを行います。
まず、クイックソートは、基準となる値を選びます。これを「枢軸」と呼びます。この枢軸を基準にして、他の値を「枢軸より小さいグループ」と「枢軸より大きいグループ」の2つのグループに分けます。
次に、分けたそれぞれのグループに対しても、同じように枢軸を選び、小さいグループと大きいグループに分けます。この作業を、グループ分けされたデータが全て1つになるまで繰り返します。それぞれのグループの中で枢軸を選ぶ、そして、小さいグループと大きいグループに分ける、この繰り返しこそがクイックソートの核心です。
クイックソートの速さの秘密は、この分割統治法と呼ばれる方法にあります。大きな問題を小さな問題に分割し、それぞれの小さな問題を解決することで、最終的に大きな問題を解決するという考え方です。
クイックソートの処理にかかる時間の目安は、データの個数をnとしたとき、平均的にはn × log nに比例します。これは、他の一般的な並び替え方法と比べて非常に高速です。例えば、データの量が多い場合や、処理の速さが求められるシステムでは、クイックソートは最適な選択肢となります。
さらに、クイックソートは、仕組みが分かりやすく、プログラムに書き起こしやすいという利点もあります。そのため、様々な場面で活用されています。例えば、順番通りに並んだデータの集まりや、表形式のデータはもちろん、情報を素早く探し出すための仕組み作りにも役立っています。クイックソートは、速さと使いやすさを兼ね備えた、非常に優れた並び替え方法と言えるでしょう。
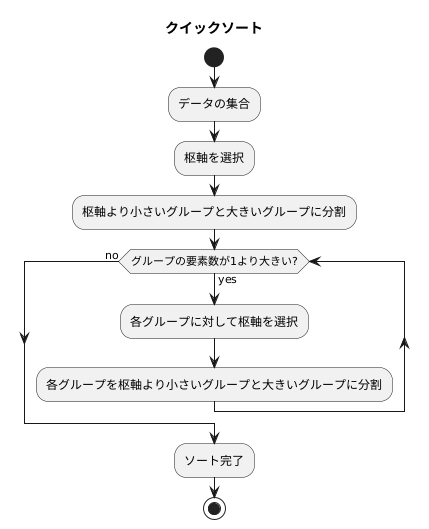
処理手順

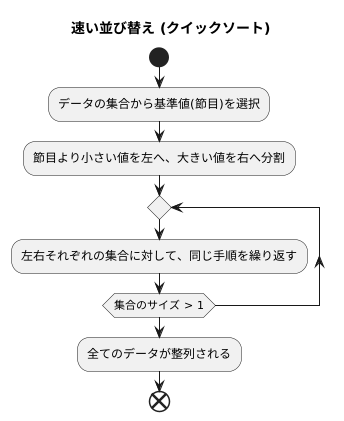
速い並び替えの手順を詳しく見ていきましょう。この速い並び替えは、基準となる値を元にして、データを繰り返し分割していく方法です。まず、データの集合の中から適当な値を選び、これを基準値とします。この基準値は、軸となる値という意味で、よく『節目』と呼ばれます。
次に、この節目を使って、データを二つに分けていきます。節目の値よりも小さい値は全て左側に、大きい値は全て右側に配置します。ちょうど、天秤を使って物を分けるように、節目という基準で軽いものと重いものを分けるイメージです。
この分割の作業が、速い並び替えの核心です。分割の方法はいくつかありますが、例えば、データの集合の先頭、真ん中、末尾の値を節目として選ぶ方法が一般的です。どの値を節目とするかによって、並び替えの速さが変わることもあります。そのため、データの特徴に合わせて、適切な方法を選ぶことが大切です。
分割が終わったら、今度は左右に分かれたそれぞれの小さなデータの集合に対して、再び同じ手順を繰り返します。つまり、左右それぞれの集合の中で、また節目を選び、小さい値を左に、大きい値を右に配置していきます。このように、分割を繰り返すことで、データの集合はどんどん小さくなっていきます。まるで、大きな石を細かく砕いていくように、データが徐々に整理されていきます。
そして最後には、全てのデータが正しい順序に配置されます。このように、速い並び替えは、節目となる値を基準にした分割と、分割したものをさらに分割していく繰り返しの手順によって、効率よくデータを並び替えることができるのです。
計算量

計算量は、ある問題を解くために必要な計算の手間を数値で表したものです。問題の規模が大きくなるにつれて、計算の手間がどのように増えていくのかを示す指標であり、効率的な方法を見つける上で重要な役割を担います。
例えば、クイックソートという並び替えの方法を考えてみましょう。この方法は、基準となる値(ピボット)を選び、それより小さい値と大きい値に分ける操作を繰り返すことで、データを順番に並べ替えます。データの数をnとすると、クイックソートの計算量は、平均的にはnかけるlog nに比例します。これは、比較操作の回数がnかけるlog n程度になることを意味し、非常に効率の良い方法と言えます。
しかし、常に効率が良いとは限りません。最悪の場合、計算量はnの2乗に比例してしまうことがあります。これは、ピボットの選び方が悪い場合に起こります。例えば、既に順番に並んでいるデータに対して、一番小さい値や一番大きい値をピボットに選んでしまうと、分割がうまくいかず、計算の手間が大きくなってしまいます。
このような事態を避けるためには、ピボットの選び方を工夫する必要があります。例えば、無作為にピボットを選んだり、幾つかの値の中央値をピボットとして使う方法があります。他にも、データの並び方に偏りがある場合は、その偏りを考慮したピボット選択を行うことで、最悪の場合でも計算量をnかけるlog nに近づけることができます。このように、適切な工夫をすることで、計算量を小さく抑え、処理速度の向上を図ることができます。
| ソート方法 | 平均計算量 | 最悪計算量 | ピボット選択と計算量の関係 |
|---|---|---|---|
| クイックソート | O(n log n) | O(n^2) | ピボットの選び方が悪い場合(例:既にソート済みのデータに対して最小値や最大値をピボットに選ぶ)に最悪計算量になる |
| ピボット選択の工夫例:ランダム選択、中央値、データの偏りを考慮した選択 | |||
長所と短所

クイックソートは、名の通り速い整列方法として知られています。その速さの秘密は、計算量の少なさです。データの数がn個あるとき、平均してnかけるデータ数の対数に比例した回数で整列が完了します。これは、とても効率が良いことを意味しており、たくさんのデータを扱う際に力を発揮します。例えば、会員数が多い通販サイトで顧客情報を年齢順に並べ替えるといった作業を想像してみてください。クイックソートなら、膨大な顧客データでも素早く整列できます。また、プログラムに書き起こすのも比較的簡単です。複雑な手順を踏む必要がないため、誰にでも理解しやすく、扱いやすい整列方法と言えるでしょう。
しかし、クイックソートにも弱点がないわけではありません。データの並び方によっては、最悪の場合、計算量がnの2乗に比例してしまうことがあります。これは、データの数が増えるほど、処理に時間がかかることを意味します。この問題を引き起こす原因の一つに、基準となる値(ピボット)の選び方があります。ピボットの選び方次第で、整列の効率が大きく変わってきます。そのため、適切なピボットを選ぶ方法を工夫する必要があります。もう一つの弱点は、同じ値を持つデータの順番が、整列後も保持されるとは限らないことです。例えば、同点の競技参加者を背番号順に並べたデータに対してクイックソートを行うと、整列後に背番号順ではなくなってしまう可能性があります。このように、データの順番を保ちたい場合は、別の整列方法を検討する必要があるでしょう。
それでも、クイックソートは多くの場面で役立つ整列方法です。特に、データの性質が事前にわからない場合や、平均的な処理速度を重視する場合は、クイックソートが有効な選択肢となります。その速さと汎用性の高さから、様々な場面で活躍しているのです。
| 項目 | 内容 |
|---|---|
| 名称 | クイックソート |
| 特徴 | 高速な整列方法 |
| 計算量(平均) | n log n |
| メリット |
|
| デメリット |
|
| 弱点の原因 | ピボットの選び方 |
| 適用例 | 会員数が多い通販サイトでの顧客情報の年齢順ソート |
| 有効な場面 | データの性質が事前にわからない場合、平均的な処理速度を重視する場合 |
他の手法との比較

様々な順番替えの方法の中から、どれを選ぶかは大切なことです。それぞれに得意なところ、不得意なところがあります。ここでは、クイックソートと他の方法を比べて、どんな時にクイックソートが適しているのかを見ていきましょう。
まず、泡の様に順番を上げていく泡ソートや、順番にカードを並べるようにデータを扱う挿入ソートを考えてみましょう。これらの方法は、仕組みは単純で分かりやすいのですが、データの数が多くなると時間がかかってしまいます。データの数が二乗に比例して時間がかかるため、たくさんのデータを扱う場合は向きません。
次に、分割して統治するマージソートを見てみましょう。マージソートは、クイックソートと同じように、平均的にはデータの数とデータの数の対数の積に比例する時間で順番替えができます。つまり、非常に速いということです。しかし、マージソートには、クイックソートにはない特徴があります。それは、同じ値のデータの順番が、順番替えの前後で変わらないということです。これを安定ソートと言います。
もう一つ、高速な順番替えの方法として、積み重ねていくヒープソートがあります。これも、平均的にはデータの数とデータの数の対数の積に比例する時間で順番替えができます。しかし、クイックソートに比べると仕組みが複雑で、理解するのも、実際にプログラムを作るのも難しくなります。
このように、どの順番替えの方法にも、良い点と悪い点があります。扱うデータの特徴や、どれくらい速く処理したいかによって、最適な方法を選ぶことが大切です。クイックソートは、平均的に見て処理速度が速く、プログラムも比較的簡単に作れるため、多くの場合で良い選択となります。
| ソート方法 | 計算量 | 特徴 | 長所 | 短所 |
|---|---|---|---|---|
| バブルソート | O(n^2) | – | 単純で分かりやすい | データが多いと遅い |
| 挿入ソート | O(n^2) | – | 単純で分かりやすい | データが多いと遅い |
| マージソート | O(n log n) | 安定ソート | 高速 | – |
| ヒープソート | O(n log n) | – | 高速 | 複雑で実装が難しい |
| クイックソート | O(n log n) | – | 高速、比較的簡単 | – |
まとめ

並び替えの処理手順の中でも、とりわけ高速で使いやすい手法として知られるのが、クイックソートです。この手法は、基準となる値(ピボット)を巧みに用いて、データを分割しながら整理していく方法で、分割統治法と呼ばれています。
クイックソートの処理速度は、平均してデータの個数(n)と、その対数の積(n log n)に比例します。これは、非常に効率的な処理速度と言えるでしょう。データの量が増えても、処理時間が極端に増えることはありません。
この処理速度は、ピボットの選び方によって変化します。ピボットの選択方法によっては、まれに処理速度が遅くなる場合も考えられます。しかし、適切な方法を用いることで、処理速度の低下を抑えることができます。
クイックソートは、安定ソートではありません。つまり、同じ値を持つデータの順番が、並び替え後に入れ替わる可能性があります。しかし、高速で汎用性が高いという長所から、様々な場面で活用されています。
大量のデータを効率的に並び替えたい場合や、平均的な処理速度を重視する場合、クイックソートは最適な選択と言えるでしょう。他の並び替え手法と比較し、それぞれの特性を理解した上で、適切な手法を選ぶことが大切です。クイックソートは、優れた性能と汎用性により、これからも様々な場面で利用されていくと考えられます。
| 項目 | 説明 |
|---|---|
| 手法名 | クイックソート |
| 処理手順 | 分割統治法(ピボットを用いてデータを分割) |
| 平均処理速度 | n log n |
| 処理速度への影響 | ピボットの選び方 |
| 安定ソート | 非安定ソート |
| メリット | 高速、汎用性が高い |
| デメリット | ピボットの選び方によっては処理速度が低下する可能性、安定ソートではない |
| 適した状況 | 大量データの効率的な並び替え、平均的な処理速度を重視する場合 |
