Mini-Max法:ゲーム戦略の基礎

AIを知りたい
先生、「ミニマックス法」って、難しそうだけど、どんな考え方なんですか?

AIエンジニア
そうですね、ゲームで自分が一番有利になるように、相手が不利になるように考える方法です。例えば、オセロを想像してみてください。自分が白、相手が黒だとします。

AIを知りたい
はい、オセロなら分かります。自分の白を増やして、相手の黒を減らしたいです。

AIエンジニア
そうです。ミニマックス法では、自分が白を置く時、一番多く白にできる場所を探します。そして、相手が黒を置く時は、黒が一番少なくなる場所を相手が選ぶと仮定して、その上で自分が一番白を増やせる場所を探します。これを交互に繰り返すことで、最終的に自分が一番有利になるように手を決めるんです。
Mini-Max法とは。
コンピュータがゲームでどう戦うかを考える方法の一つに「ミニマックス法」というものがあります。これは、自分の番では一番いい手を選び、相手の番では相手にとって一番悪い手になるように考える方法です。自分の得点を最大に、相手の得点を最小にするように、つまり、最大と最小を考えていくので「ミニマックス法」と呼ばれています。
はじめに

勝負事で、どうすれば一番良い手を打てるのか、誰もが一度は考えたことがあるでしょう。常に最善の一手を考えることは、ゲームで勝つための鍵となります。相手の手の内を読み、自分の勝ちへの道筋を立てることは、多くのゲームで重要です。このような場面で力を発揮するのが、「ミニマックス法」と呼ばれる考え方です。ミニマックス法は、ゲームの展開を予測し、最も有利な行動を選ぶための計算方法で、人工知能の分野で広く使われています。
このミニマックス法は、ゲームを木構造で捉え、各局面での点数を計算することで最善手を探します。木構造とは、枝分かれした図のようなもので、最初の状態から可能な手を枝分かれさせて、相手の出方、それに対する自分の出方、と交互に展開を書き出していくことで作られます。そして、この木の葉の部分、つまり最終的な勝敗が決まった状態に点数を付けます。例えば、自分が勝った状態には高い点数、負けた状態には低い点数を付けます。
次に、この点数を木の枝を逆に辿って計算していきます。自分の番では、可能な手の中から最も高い点数の手を選び、相手の番では、可能な手の中から最も低い点数の手を選びます。相手は、自分にとって不利な手、つまり点数が低い手を選ぶと想定するからです。このように、交互に高い点数と低い点数を選んでいくことで、最初の状態に戻ってきた時に、最も有利な一手、つまり点数が最大となる一手を選ぶことができます。
例えば、三目並べのような簡単なゲームであれば、全ての展開を計算し、ミニマックス法を用いて最善手を見つけることが可能です。しかし、将棋や囲碁のような複雑なゲームでは、全ての展開を計算することは現実的に不可能です。そのため、ある程度の深さまで木構造を展開し、その先を予測する評価関数などを用いて計算を簡略化する必要があります。この記事では、ミニマックス法の概念をさらに詳しく説明し、具体的な例を挙げて、その仕組みを分かりやすく解説します。
交互の手順

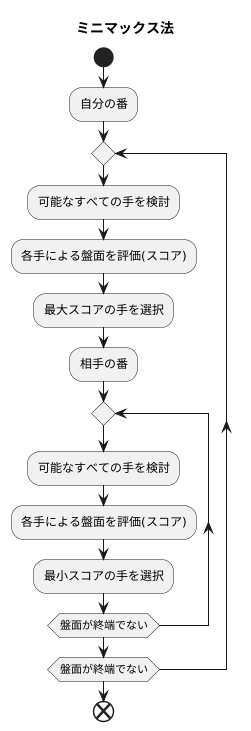
二人対戦型の遊戯において、交互に手順を進める様を「交互の手順」と呼びます。この手順を扱う手法の一つに「ミニマックス法」があります。ミニマックス法は、両者が常に自分の得点を最大化しようとするという前提に基づいて手順を解析します。つまり、自分の番では最も有利となる手を選び、相手の番では最も不利となる手を想定します。
自分の番では、可能な全ての手を検討し、それぞれの手に対応した盤面を評価します。この評価はスコアと呼ばれる数値で行われ、高いほど有利、低いほど不利となります。あらゆる可能な手のうち、最も高いスコアとなる手を選びます。これが自分の得点の最大化にあたります。
一方、相手の番では、相手も同様に自分の得点を最大化しようとします。つまり、自分にとっては最も低いスコアとなる手を選んでくる、と想定します。この想定に基づき、相手が選ぶであろう最も不利な手、すなわち自分にとっての最低スコアとなる手を見極めます。これが相手の得点の最大化、すなわち自分にとっての最小化にあたります。
このように、ミニマックス法は、自分の番では最大のスコアとなる手を選び、相手の番では最小のスコアとなる手を想定することで、交互の手順における最適な戦略を導き出します。この最大化と最小化を交互に繰り返すことから「ミニマックス」という名前が付けられています。この手法を用いることで、常に最善の手を打ち続けることが可能となり、遊戯における勝利の可能性を高めることができます。
木構造による表現

勝負を決める手順を考える時、木構造を使うと分かりやすくなります。木構造とは、根っこから枝が伸び、さらにその枝からまた枝が伸びていくような構造です。まるで本物の木のように、階層的に物事を整理できます。
ゲームを考えてみましょう。今のゲームの状態が木の根っこにあたります。そこから、プレイヤーができる様々な行動が、枝分かれしていく様子で表されます。例えば、将棋であれば、次に駒をどこに動かすかの選択肢が枝になります。それぞれの枝の先には、その行動の結果、どうなるかという新しいゲームの状態が作られます。これが木の節にあたります。
このように、行動の選択肢と、その結果の状態が、次々に枝分かれして木構造を作っていきます。この木構造全体が、ゲームの進行を表現しているのです。最初の状態から、様々な行動を選び、その結果としてどんな状態になるかを、木構造でたどることができます。
この木構造を使って、最善の手を探す方法が、ミニマックス法です。ミニマックス法は、相手の手も考えながら、自分の得点を最大化する行動を見つけ出します。具体的には、木構造の枝をたどりながら、それぞれの状態での評価値を計算していきます。そして、相手が自分の得点を最小にするように行動すると仮定して、自分の得点が最大になる行動を選択します。
つまり、木構造はゲームの進行を分かりやすく表現するだけでなく、最善の手を見つけるための土台としても役立つのです。
最小と最大の評価

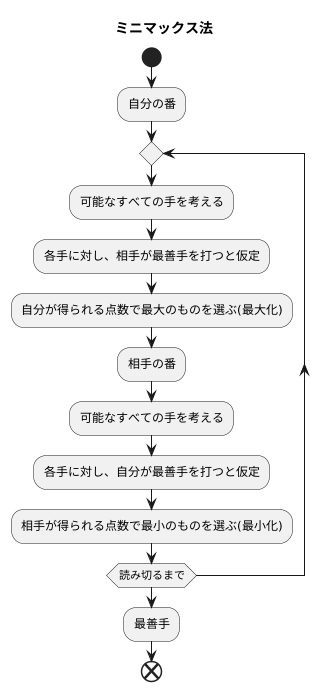
最小最大法という名前は、この方法が、最小化と最大化を交互に繰り返すことから来ています。この方法は、ゲームなどの対戦において、自分の番と相手の番を交互に繰り返しながら、最善の手を見つけるために使われます。
まず、自分の番では、次に可能な全ての手を考えます。それぞれの手を打った場合、次に相手にどのような手が打たれるかを予測します。そして、相手が最善の手を打ってきた場合に、自分が得られる点数のうち、最も高い点数を持つ手を選びます。つまり、最悪の状況でも、なるべく良い結果を得られるように考えて手を選びます。
次に、相手の番では、相手も同様に考えます。相手は、次に可能な全ての手の中から、自分が最善の手を打った場合に、相手が得られる点数のうち、最も低い点数を持つ手を選びます。つまり、相手は、こちらが最善を尽くしても、なるべく悪い結果になるように考えて手を選びます。
このように、自分の番では最大の点数を選ぶことを最大化、相手の番では最小の点数を選ぶことを最小化と言い、この最大化と最小化を交互に繰り返すことで、最終的に最善の手を見つけ出します。
たとえば、将棋や囲碁のようなゲームで、何手先まで読むかを決めて、その範囲でこの最小最大法を使うことで、現時点での最善手を見つけることができます。この方法は、相手が常に最善の手を打つと仮定しているので、相手がミスをした場合には、さらに有利な結果を得られる可能性があります。また、読む手の数を増やすほど、より正確な最善手を見つけられる可能性が高まりますが、計算量も増えるため、実際には、読める手の数と計算時間のバランスを考える必要があります。
具体的なゲームへの適用

勝負が交互に行われ、先を読むことが重要な様々な遊びに、ミニマックス法と呼ばれる考え方が役立ちます。例えば、将棋や囲碁、チェス、三目並べなどがその例です。これらの遊びには、盤面の状態や可能な指し手が明確に決まっているという共通点があります。このおかげで、ミニマックス法を使って、次にどんな手を指すのが最善かを調べることができます。
ミニマックス法は、自分が指す手を決める時に、相手がどのように反撃してくるかを想定しながら、最善の手を探す方法です。具体的には、自分が指せる全ての手を調べ、それぞれの手に対応して相手が指せる全ての手をさらに調べます。この時、相手は自分にとって不利になるような手を選ぶと想定します。こうして何手か先まで読み進めることで、最終的に自分が最も有利になるような手を選ぶことができます。
しかし、この方法は、遊びが複雑になるほど、調べる手数の組み合わせが爆発的に増えてしまうという問題点があります。例えば、囲碁のように盤面が広く、可能な指し手が非常に多い遊びでは、ミニマックス法だけで最善手を探すのは現実的ではありません。このような場合には、どこまで先を読むかを制限したり、明らかに不利な指し手を途中で無視するなどの工夫が必要です。また、盤面の評価方法を工夫することで、より効率的に探索を行うこともできます。
ミニマックス法は、遊びをプログラムで動かす時に、コンピュータに考えさせるための基本的な考え方となっています。遊びの複雑さやコンピュータの性能に合わせて、様々な改良が加えられて使われています。最近では、このミニマックス法をさらに発展させた、モンテカルロ木探索などの新しい方法も使われるようになってきています。これらの技術により、コンピュータは人間に匹敵する、あるいは人間を超える強さで様々な遊びをプレイできるようになっています。
| 項目 | 説明 |
|---|---|
| ミニマックス法 | 勝負が交互に行われ、先を読むことが重要な遊びで、相手がどのように反撃してくるかを想定しながら最善の手を探す方法。 |
| 適用例 | 将棋、囲碁、チェス、三目並べなど、盤面の状態や可能な指し手が明確に決まっている遊び。 |
| 方法 | 自分が指せる全ての手を調べ、それぞれの手に対応して相手が指せる全ての手を調べ、相手は自分にとって不利になるような手を選ぶと想定し、何手か先まで読み進めることで、最終的に自分が最も有利になるような手を選ぶ。 |
| 問題点 | 遊びが複雑になるほど、調べる手数の組み合わせが爆発的に増えてしまう。 |
| 対策 | 先を読む深さを制限する、明らかに不利な指し手を途中で無視する、盤面の評価方法を工夫する。 |
| 発展 | モンテカルロ木探索など。 |
| 応用 | コンピュータに考えさせるための基本的な考え方として、様々な改良が加えられて使われている。 |
発展的な手法

勝負を決める手順を考える時、基本となる考え方に「ミニマックス法」というものがあります。この方法は、自分が最良の手を選び、相手は自分にとって最悪の手を選ぶという前提で、可能な限り先の手まで読んで最善の手を導き出す方法です。しかし、この方法では、先を読むほど考える量が増え、複雑なゲームでは限界があります。そこで、ミニマックス法をより良くするための工夫がいくつか考えられています。
その一つが「αβ枝刈り」と呼ばれる方法です。これは、明らかに不利な手順を途中で切り捨てることで、考える量を減らす工夫です。例えば、自分が3通りの手順A、B、Cを考えた時、相手の手番で手順Aに対して最悪の展開を考えてみます。次に、手順Bを考えた時、相手の手番で手順Aよりも悪い展開になることが途中でわかったとします。この場合、手順B以降を考える必要はありません。なぜなら、相手は自分にとってより悪い展開となる手順Aを選ぶはずだからです。このように、無駄な部分を切り捨てることで、計算の手間を大きく減らすことができます。
もう一つの工夫は、局面の良し悪しを判断する「評価関数」の精度を上げることです。評価関数は、現在のゲームの状態がどれくらい有利かを数値で表すものです。この関数が正確であれば、より的確な手順を選ぶことができます。例えば、将棋で「駒の数」だけを評価の基準にすると、王手がかかっているのに駒が多い方が有利と判断してしまいます。そこで、「王手」や「駒の働き」なども考慮することで、より正確な評価が可能になります。
これらの改良を組み合わせることで、ミニマックス法はさらに強力になります。複雑なゲームでも、より深く読み、より良い手順を見つけることが可能になるのです。
| ミニマックス法の改良 | 説明 | 例 |
|---|---|---|
| αβ枝刈り | 明らかに不利な手順を途中で切り捨てることで、計算量を削減する。 | 3つの手順A,B,Cのうち、BがAより悪いと途中で判明した場合、B以降の展開を検討する必要はない。 |
| 評価関数の精度向上 | 局面の良し悪しを判断する評価関数をより正確にすることで、的確な手順選択を可能にする。 | 将棋において、駒の数だけでなく、王手や駒の働きも考慮する。 |
