平均絶対偏差:データのばらつきを測る

AIを知りたい
先生、「平均絶対偏差」って、どういう意味ですか?よく分からなくて…

AIエンジニア
簡単に言うと、データのばらつき具合を見るためのものだよ。それぞれのデータが、平均値から平均でどれくらい離れているかを表しているんだ。

AIを知りたい
平均値からの距離…ですか?もう少し具体的に教えてもらえますか?

AIエンジニア
例えば、テストの点数を考えてみよう。平均点が70点で、Aさんは60点、Bさんは80点だったとする。AさんとBさんの点数と平均点との差はどちらも10点だよね。この差の絶対値を平均したものが平均絶対偏差になるんだ。この例では10点だね。
平均絶対偏差とは。
人工知能の分野でよく使われる言葉である「平均絶対偏差」について説明します。この言葉は、数学や統計学、機械学習の分野で使われており、平均との差の絶対値の平均を意味します。簡単に「平均偏差」や「絶対偏差」と呼ばれることもあります。
はじめに

情報を詳しく調べたり整理したりする作業の中で、データがどれくらい散らばっているかを理解することはとても大切です。平均値だけではデータの全体像を捉えきれない場合がよくあります。例えば、ある地域の平均年収が500万円だったとしましょう。一見すると、そこそこ豊かな地域のように思えますが、実は少数の高所得者によって平均値が押し上げられているかもしれません。大部分の住民は年収300万円で、ごく一部の人が1000万円以上の年収を得ている可能性も考えられます。このような状況では、平均年収という一つの数字だけで判断すると、実態を見誤ってしまう危険性があります。
そこで、データの散らばり具合を測る尺度として、平均絶対偏差が役に立ちます。平均絶対偏差とは、それぞれのデータが平均値からどれくらい離れているかを平均した値です。具体的な計算方法は、まず各データと平均値の差を計算します。次に、その差の絶対値を求めます。絶対値とは、マイナスの符号を取り除いた値のことです。最後に、これらの絶対値をすべて足し合わせ、データの個数で割ります。こうして求められた平均絶対偏差は、データの散らばり具合を直感的に理解するのに役立ちます。平均絶対偏差が大きいほど、データは平均値から遠く離れた値が多く、散らばりが大きいことを示しています。逆に、平均絶対偏差が小さい場合は、データは平均値の近くに集まっており、散らばりが小さいことを意味します。
平均絶対偏差を理解することで、データの分布や特徴をより深く把握することができます。平均値だけでなく、平均絶対偏差も合わせて見ることで、データの背後にある真の姿が見えてきます。例えば、二つの地域の平均年収が同じでも、平均絶対偏差が大きく異なる場合があります。これは、収入の分布に大きな違いがあることを示唆しています。平均絶対偏差を用いることで、このような違いを明確に捉えることができるのです。
| 用語 | 説明 | 例 |
|---|---|---|
| 平均値 | データの合計をデータの個数で割った値 | 地域の平均年収500万円 |
| 平均絶対偏差 | 各データと平均値の差の絶対値の平均 | 高所得者と低所得者の差が大きい場合、平均絶対偏差は大きくなる |
| データの散らばり | データが平均値からどれくらい離れているか | 平均絶対偏差が大きいほど、データの散らばりが大きい |
計算方法

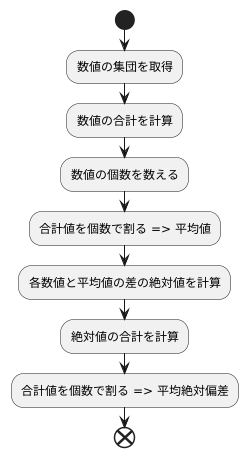
計算方法は、比較的単純で、順を追って行うことで容易に理解できます。まず、与えられた数値の集団全体の平均、つまり中心となる値を求めます。これは、集団に含まれる数値全てを合計し、その合計値を数値の個数で割ることで算出できます。
次に、個々の数値と先に求めた平均値との差を計算します。この差は、正の値の場合も負の値の場合もありますが、ここでは差の大きさにのみ注目するため、それぞれの差の絶対値を求めます。絶対値とは、数値の符号を無視した大きさのことです。例えば、-3の絶対値は3、+3の絶対値も3です。
最後に、これらの絶対値を全て合計し、その合計値を絶対値の個数、つまり元の数値の個数で割ります。こうして得られた値が、平均絶対偏差です。平均絶対偏差は、数値の集団が平均値からどれくらい離れているかを表す指標です。この値が大きいほど、数値の集団は平均値から散らばっている、つまりばらつきが大きいと言えます。逆に、この値が小さいほど、数値の集団は平均値の近くに集まっている、つまりばらつきが小さいと言えます。
例として、{2, 4, 6, 8}という数値の集団を考えてみましょう。まず、平均値は(2+4+6+8)/4 = 5です。次に、各数値と平均値5との差の絶対値は、|2-5|=3, |4-5|=1, |6-5|=1, |8-5|=3となります。最後に、これらの絶対値の平均値を計算すると、(3+1+1+3)/4 = 2となります。したがって、この数値集団の平均絶対偏差は2です。これは、この数値集団が平均値5から平均的に2だけ離れていることを示しています。
標準偏差との違い

データのばらつき具合を知ることは、統計分析において非常に大切です。データがどれくらい平均値から離れているのかを知ることで、データの性質をより深く理解することができます。データのばらつき具合を示す指標はいくつかありますが、よく使われるものとして標準偏差と平均絶対偏差があります。どちらもデータの散らばり具合を表すものですが、計算方法と外れ値への強さに違いがあります。
標準偏差は、まず各データの値と平均値との差を計算します。次に、その差を二乗し、すべてのデータの二乗した差の平均値を求めます。最後に、その値の平方根を計算することで標準偏差が得られます。二乗計算を行うため、平均値から大きく離れた値、つまり外れ値の影響を大きく受けるという特徴があります。例えば、ほとんどのデータが平均値付近に集まっているにもかかわらず、一つだけ極端に大きな値や小さな値がある場合、標準偏差は大きく変化します。
一方、平均絶対偏差は、各データの値と平均値との差の絶対値を計算し、その平均値を求めることで得られます。絶対値を用いるということは、差の正負を無視して、平均値からの距離のみを考慮するということです。そのため、標準偏差と比べて外れ値の影響を受けにくいという特徴があります。先ほどの例のように、極端な値があったとしても、他のデータが平均値付近に集まっていれば、平均絶対偏差はそれほど大きな値になりません。
このように、標準偏差と平均絶対偏差は計算方法が異なり、外れ値への影響の受けやすさが違います。そのため、分析対象のデータに外れ値が含まれているかどうかを考慮して、どちらの指標を用いるかを判断することが重要です。外れ値の影響を受けにくい指標が必要な場合は、平均絶対偏差の方が適していると言えます。
| 指標 | 計算方法 | 外れ値の影響 |
|---|---|---|
| 標準偏差 | 各データと平均値の差を二乗し、その平均の平方根 | 影響を受けやすい |
| 平均絶対偏差 | 各データと平均値の差の絶対値の平均 | 影響を受けにくい |
活用事例

平均絶対偏差は、データのばらつき具合、つまりデータが平均値からどれくらい離れているかを示す指標であり、様々な分野で活用されています。
金融分野では、投資におけるリスク評価に役立ちます。例えば、複数の投資先の過去のリターンデータから平均絶対偏差を計算することで、それぞれの投資先の価格変動の大きさを比較できます。平均絶対偏差が小さい投資先は価格変動が少なく安定している傾向があり、リスクが低いと判断できます。一方で、平均絶対偏差が大きい投資先は価格変動が激しく、リスクが高いと判断できます。このように、平均絶対偏差を用いることで、投資家はより的確にリスクを把握し、投資判断を行うことができます。
製造業では、製品の品質管理に活用されます。例えば、製造ラインで生産される製品の寸法や重量などのデータを収集し、平均絶対偏差を計算します。平均絶対偏差が小さい場合は、製品の品質が安定していることを示します。逆に、平均絶対偏差が大きい場合は、製品の品質にばらつきがあることを示し、製造工程に何らかの問題が発生している可能性を示唆します。この指標を用いることで、製造工程の改善や品質の向上に繋げることができます。
気象学では、気温や降水量などの気象データの変動を分析するために利用されます。ある地域の年間平均気温と日々の気温の平均絶対偏差を計算することで、その地域の気温の安定性を評価できます。平均絶対偏差が小さい場合は、年間を通して気温が安定していることを示し、大きい場合は、気温の変化が大きいことを示します。
社会学の分野でも、例えば、世帯収入のばらつきを分析するために利用できます。地域ごとの世帯収入の平均絶対偏差を計算することで、その地域の所得格差を把握できます。平均絶対偏差が小さい場合は、世帯収入のばらつきが小さく、所得格差が小さいことを示し、大きい場合は、世帯収入のばらつきが大きく、所得格差が大きいことを示します。このように、様々な分野で活用される平均絶対偏差は、データの特性を深く理解し、適切な判断を行うための重要なツールと言えるでしょう。
| 分野 | 活用例 | 平均絶対偏差の意味 |
|---|---|---|
| 金融 | 投資におけるリスク評価 | 小さい:リスクが低い、大きい:リスクが高い |
| 製造業 | 製品の品質管理 | 小さい:品質が安定、大きい:品質にばらつき |
| 気象学 | 気温や降水量などの気象データの変動分析 | 小さい:気象が安定、大きい:気象の変化が大きい |
| 社会学 | 世帯収入のばらつき分析 | 小さい:所得格差が小さい、大きい:所得格差が大きい |
まとめ

データのばらつき具合、つまり値がどれくらい平均から離れているかを知ることは、データ分析においてとても大切です。そのばらつき具合を測る尺度の一つに、平均絶対偏差があります。これは、各データの値が平均値からどれくらい離れているかを絶対値で表し、その平均値を取ったものです。
平均絶対偏差の計算は比較的単純です。まず、全てのデータの平均値を求めます。次に、各データの値と平均値の差を計算し、その差の絶対値を取ります。最後に、それらの絶対値の平均値を計算することで、平均絶対偏差が求まります。計算が簡単なため、データの全体像を素早く把握したい時に役立ちます。
平均絶対偏差の大きな利点の一つは、外れ値の影響を受けにくいことです。外れ値とは、他のデータから大きく離れた極端な値のことです。標準偏差などの尺度は、この外れ値の影響を大きく受けてしまうことがありますが、平均絶対偏差は絶対値を用いるため、外れ値の影響を軽減することができます。つまり、一部の極端な値に左右されず、データのばらつきを安定して評価できるのです。
データのばらつき具合を表す尺度として、標準偏差がよく知られています。標準偏差は、各データの値と平均値の差を二乗し、その平均値の平方根を取ったものです。標準偏差と比較すると、平均絶対偏差は計算が容易で、外れ値の影響を受けにくいという特徴があります。これらの尺度を組み合わせて使うことで、データの特性をより深く理解することができます。例えば、標準偏差が大きく、平均絶対偏差が小さい場合は、少数の外れ値がデータのばらつきに大きく影響している可能性を示唆しています。
平均絶対偏差は、様々な分野で活用されています。例えば、金融業界では、投資のリスク評価に用いられます。製造業では、製品の品質管理に役立ちます。また、マーケティング分野では、顧客の購買行動分析などに利用されています。このように、平均絶対偏差は、データに基づいた的確な判断をする上で、強力なツールとなるのです。
| 尺度 | 計算方法 | 特徴 | 利点 | 欠点 | 用途 |
|---|---|---|---|---|---|
| 平均絶対偏差 | 1. 全データの平均値を求める 2. 各データと平均値の差の絶対値を求める 3. それらの絶対値の平均値を計算する |
外れ値の影響を受けにくい | 計算が容易 データの全体像を素早く把握できる 安定したばらつきの評価が可能 |
標準偏差と比べ、情報量が少ない場合がある | 金融業界:投資のリスク評価 製造業:製品の品質管理 マーケティング:顧客の購買行動分析 |
| 標準偏差 | 1. 各データと平均値の差の二乗を求める 2. それらの二乗の平均値を求める 3. 平均値の平方根を計算する |
外れ値の影響を受けやすい | データのばらつきをより詳細に表現できる | 計算が複雑 外れ値に大きく影響される |
多くの統計分析で使用 |
