マルコフ決定過程モデル:未来予測への道

AIを知りたい
『マルコフ決定過程モデル』って、難しそうですね。現在の状態と変化する確率だけで次の状態が決まるっていうのはなんとなくわかるのですが、過去は関係ないってどういうことでしょうか?

AIエンジニア
いい質問ですね。例えば、今日雨が降ったとして、明日雨が降る確率は、昨日雨が降っていたかどうかには関係なく、今日の天気(雨)だけを考慮するということです。過去に雨が何日続いていようと、明日の天気への影響はないと考えるのがマルコフ過程モデルです。

AIを知りたい
なるほど。では、『マルコフ決定過程モデル』はそれにどんなことを付け加えたものなのですか?

AIエンジニア
『マルコフ決定過程モデル』は、単に状態が変化するだけでなく、そこに『行動』という要素が加わります。例えば、ロボットが部屋を掃除する場合、現在の位置(状態)で、どの方向に動くか(行動)を選択すると、次の位置(状態)が決まります。この『行動』を選択する部分がマルコフ決定過程モデルで重要になります。
マルコフ決定過程モデルとは。
『マルコフ決定過程モデル』という、人工知能に関係する言葉について説明します。このモデルは、ある状況である行動をとった時に、別の状況に変化していく仕組みを表したものです。変化は確率的に、つまり偶然に左右されることもあります。まず、『マルコフ過程モデル』というものがあって、これは未来の状況が過去の状況とは関係なく、今の状況と変化する確率だけで決まるというものです。マルコフ決定過程モデルは、これにどういう行動をとるかという考え方を加えたものになります。
マルコフ決定過程モデルとは

マルコフ決定過程モデルは、不確実な状況で、次に何をすればよいかを決めるときに役立つ強力な道具です。このモデルは、現在の状況に応じて行動を選ぶと、将来の状況がどのように変化するかを確率で表します。ちょうど、サイコロを振るとどの目が出るかわからないように、将来の状況も確実には予測できませんが、ある程度の確率で変化していく様子を捉えることができます。
このモデルは、現在の状況だけが将来の状況に影響を与えるという考え方を持っています。つまり、過去の状況は関係なく、今の状況さえわかれば、次に何が起こるかを予測できるということです。これをマルコフ性といいます。この性質のおかげで、計算が比較的簡単になり、様々な分野で使われています。例えば、ロボットがどのように動けば目的地にたどり着けるか、倉庫にどれだけの商品を保管しておけばよいか、お金をどのように運用すれば利益を増やせるか、といった問題を解決するのに役立ちます。
マルコフ決定過程モデルは、状態、行動、遷移確率、報酬という四つの要素でできています。状態とは、システムが取りうる様々な状況のことです。例えば、ロボットの位置や、倉庫の在庫量、現在の資産額などが状態にあたります。行動とは、それぞれの状態で選べる選択肢のことです。ロボットの進む方向、商品の発注量、投資する商品の種類などが行動にあたります。遷移確率は、ある状態で特定の行動をとったときに、次にどの状態に移るかの確率です。例えば、ロボットが北に進むと決めたときに、実際に北に進む確率、倉庫に商品を発注したときに、その商品が予定通り届く確率などです。最後は報酬です。報酬は、ある状態で特定の行動をとったときに得られる利益や損失のことです。ロボットが目的地に到達したときに得られる点数、商品を販売して得られる利益、投資で得られる収益などが報酬にあたります。これらの要素を組み合わせることで、どんな行動をとれば最も多くの利益を得られるか、といった最適な行動計画を立てることができます。
| 要素 | 説明 | 例 |
|---|---|---|
| 状態 | システムが取りうる様々な状況 | ロボットの位置、倉庫の在庫量、現在の資産額 |
| 行動 | それぞれの状態で選べる選択肢 | ロボットの進む方向、商品の発注量、投資する商品の種類 |
| 遷移確率 | ある状態で特定の行動をとったときに、次にどの状態に移るかの確率 | ロボットが北に進むと決めたときに、実際に北に進む確率、倉庫に商品を発注したときに、その商品が予定通り届く確率 |
| 報酬 | ある状態で特定の行動をとったときに得られる利益や損失 | ロボットが目的地に到達したときに得られる点数、商品を販売して得られる利益、投資で得られる収益 |
マルコフ過程モデルとの関係

マルコフ決定過程モデルは、名前からも想像できるように、マルコフ過程モデルと深い関わりがあります。具体的には、マルコフ決定過程モデルはマルコフ過程モデルを拡張したものと言えるでしょう。
まず、マルコフ過程モデルとは何かを見ていきましょう。マルコフ過程モデルは、システムの状態が確率的に変化していく様子を表現するモデルです。例えば、明日の天気は今日の天気に影響される確率が高いでしょう。晴れの日の翌日は晴れである確率は高く、雨の日の翌日は雨である確率も高いと考えられます。このように、ある時点の状態が次の時点の状態に影響を与える確率的な変化を捉えるのがマルコフ過程モデルです。ただし、マルコフ過程モデルでは、人の行動といった要素は考慮されていません。あくまで自然に起こる状態変化のみを対象としています。天気予報や株価予測など、様々な分野でこのモデルが活用されています。
一方、マルコフ決定過程モデルは行動という概念が導入されています。ある状態において、どのような行動をとるかによって、次の状態が確率的に決定されます。つまり、マルコフ過程モデルに行動選択という要素を加えたものがマルコフ決定過程モデルと言えるでしょう。自動運転車を例に考えてみましょう。現在の車の位置、速度、周りの車の状況などが「状態」を表すとします。この状態において、アクセルを踏む、ブレーキを踏む、ハンドルを切るといった「行動」を選択することで、次の瞬間の車の状態が変化します。マルコフ決定過程モデルはこのような状況をうまく表現できるため、自動運転における経路計画や、ロボットの行動制御など、様々な場面で応用されています。
両モデルの共通点は「マルコフ性」と呼ばれる性質にあります。これは、未来の状態が現在の状態のみによって決まり、過去の状態には影響を受けないという考え方です。この性質のおかげで、複雑な計算を比較的単純化することが可能になります。マルコフ決定過程モデルは、マルコフ過程モデルを土台とし、行動という要素を付け加えることで、より複雑な問題を扱えるように発展したモデルと言えるでしょう。
| 項目 | マルコフ過程モデル | マルコフ決定過程モデル |
|---|---|---|
| 定義 | システムの状態が確率的に変化していく様子を表現するモデル | マルコフ過程モデルに行動選択という要素を加えたモデル |
| 行動 | 考慮しない | 考慮する |
| 例 | 天気予報、株価予測 | 自動運転における経路計画、ロボットの行動制御 |
| マルコフ性 | あり | あり |
行動の概念

「行動」とは、ある状況において主体が選べる選択肢のことです。この行動の概念は、マルコフ決定過程モデルにおいて中心的な役割を果たします。マルコフ決定過程モデルとは、様々な状況の中で、どのように行動を選択すれば最も良い結果が得られるのかを数学的に考えるための枠組みです。
例えば、自動で動く機械が迷路を進む場面を想像してみましょう。この機械にとっての行動は、「前へ進む」、「後ろへ戻る」、「右へ曲がる」、「左へ曲がる」などです。それぞれの行動は、機械の次の位置に影響を与えます。「前へ進む」を選べば、機械は一つ前の場所へ移動します。他の行動を選んだ場合も同様に、機械はそれぞれの行動に対応した場所に移動します。このように、どの行動を選ぶかによって、機械の次の位置が決まるのです。行動は、システムの状態を変化させる力を持っています。
マルコフ決定過程モデルの主な目的は、長期的に見て最も良い結果を得られる行動の選び方を見つけることです。この「最も良い結果」は、数値化された「報酬」で表されます。迷路の例では、ゴールに辿り着けば高い報酬が得られ、壁にぶつかったり、同じ場所をぐるぐる回ったりする行動には低い報酬が設定されます。
最適な行動戦略を見つけるためには、どの状況でどの行動を選ぶべきかを計算する手順が必要です。この手順は、将来の状況の変化と、それによって得られる報酬を予測しながら、最適な行動の組み合わせを見つけ出します。つまり、目先の報酬だけでなく、将来得られる報酬も見積もりながら、最善の行動を決定するのです。このように、マルコフ決定過程モデルは、様々な行動とその結果を分析することで、複雑な状況下での最適な行動戦略を導き出す強力な道具となります。
状態遷移

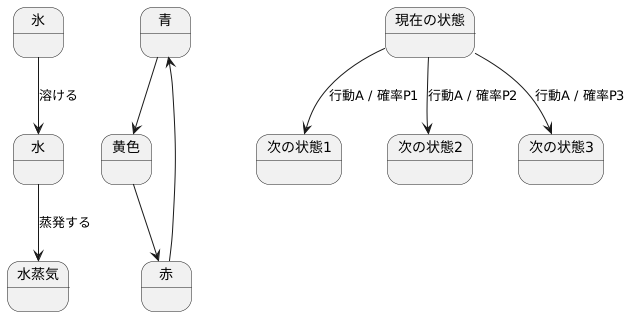
状態遷移とは、システムや物事がある状態から別の状態へと変化することを指します。例えば、信号機の色が青から黄色、そして赤へと変わるのも状態遷移の一つです。 日常生活の中でも、氷が溶けて水になる、あるいは水が蒸発して水蒸気になるといった現象も、状態遷移として捉えることができます。
特に、マルコフ決定過程モデルにおいて、この状態遷移は重要な役割を担います。このモデルでは、状態遷移は確率的に起こるものとして扱われます。つまり、現在の状態と取った行動が同じでも、次にどの状態に移るかは必ずしも決まっていません。まるでサイコロを振るように、様々な可能性の中から一つが選ばれるイメージです。
例えば、自動で動く機械が迷路を進んでいるとします。「前に進む」という指示を出しても、機械が思い通りに次の区画に進むとは限りません。センサーの誤作動や、想定外の障害物などによって、思わぬ方向に進んでしまう可能性も考えなければなりません。このような不確実性を表現するために、マルコフ決定過程モデルでは遷移確率という考え方を用います。
遷移確率とは、現在の状態と行動に基づいて、次にどの状態に移るかの確率を表す数値です。この確率は、過去の状態遷移には影響を受けません。つまり、今現在の状態と行動だけが、次の状態を決める要素となるのです。この性質をマルコフ性と呼びます。マルコフ性は、マルコフ決定過程モデルを計算しやすくする上で非常に重要な特性です。遷移確率を用いることで、様々な不確実性を含んだ状況をモデル化し、分析することが可能になります。
報酬

物事や状況を順に処理していく考え方であるマルコフ決定過程の模型では、それぞれの状況で行動を起こした時に得られる成果を数値で表した報酬を大切な要素として扱います。この報酬は、システムが目指す目的を達成するために重要な役割を果たします。
例えば、ロボットに迷路の探索をさせる場合を考えてみましょう。ロボットが目的地点に辿り着いた時には、良い結果として正の報酬を与えます。反対に、ロボットが壁にぶつかってしまった場合は、良くない結果として負の報酬を与えます。このように、状況に応じた報酬を設定することで、ロボットの行動を制御します。
では、どのようにして最適な行動の計画を立てるのでしょうか。それは、これから得られると予想される報酬の合計値を最大にするように行動を決めることです。しかし、将来得られる報酬は、今すぐ得られる報酬と同じ価値ではありません。将来の報酬は、時間の経過とともに価値が薄れていくと考えられます。この価値の減少を調整するのが割引率という数値です。
割引率は、将来の報酬を現在の価値に換算するために使われます。割引率の値が小さいほど、将来の報酬は現在の価値に比べて低く評価されます。これは、将来何が起こるかわからないため、確実な現在の成果をより重視するという考えに基づいています。
マルコフ決定過程の模型では、これらの報酬と割引率を計算に組み込むことで、最も効果的な行動方針を見つけることができます。最良の行動方針は、現在の状況だけでなく、将来の状況の変化と報酬の予測も踏まえて決定されます。このように、将来の予測に基づいて現在の行動を決定することで、最終的に最大の成果を得られるように計画を立てます。
