深さ優先探索:奥深くまで探求

AIを知りたい
『深さ優先探索』って、どういう探索方法ですか?

AIエンジニア
そうですね。迷路を想像してみてください。まず、一つの道を、行き止まりになるまで進みます。行き止まりにぶつかったら、分かれ道まで戻り、まだ進んでいない別の道を、また行き止まりまで進む。これを繰り返す探索方法です。

AIを知りたい
なるほど。ひたすら真っすぐ進んで、ダメだったら戻るんですね。でも、広い迷路だと、戻るのにも時間がかかりそうですね。

AIエンジニア
その通りです。メリットとしては、比較的単純な手順で実現できること、そしてメモリをあまり使わないことがあります。しかし、深い階層まで探索してしまうと、時間と資源の無駄遣いになる可能性もあるため、注意が必要です。
深さ優先探索とは。
人工知能の用語で『深さ優先探索』というものがあります。これは、道を探す方法の一つで、まず行き止まりまで、分かれ道に戻らずに進んでいくやり方です。行き止まりに着いたら、分かれ道まで戻り、そこからまた別の行き止まりまで進んでいきます。これを繰り返すことで、道をくまなく探します。
はじめに

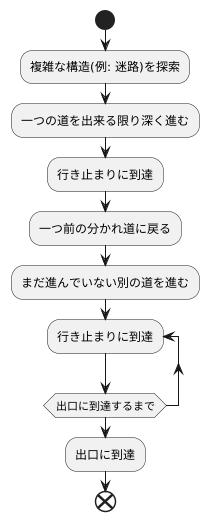
深さ優先探索とは、迷路を解くように、複雑な構造の中を隅々まで調べ上げる方法です。 例として、複雑に入り組んだ迷路を考えてみましょう。この迷路から脱出するためには、まず一つの道を出来る限り奥深く進んでいきます。そして、行き止まりに突き当たったら、一つ前の分かれ道まで戻り、まだ進んでいない別の道を進んでいきます。これを繰り返すことで、最終的には迷路の出口にたどり着くことができます。深さ優先探索もこれと同じ考え方で、複雑な構造の中を、可能な限り深く掘り下げて探索していきます。 このような探索方法は、特にグラフや木構造と呼ばれる、 interconnected network のようなデータ構造を調べる際に役立ちます。これらの構造は、節と枝が複雑に絡み合って構成されており、深さ優先探索を用いることで、特定の情報を見つけ出したり、構造全体を漏れなく調べ上げたりすることができます。 例えば、一族の家系図を思い浮かべてみてください。家系図は、先祖から子孫へと枝分かれしていく木構造です。深さ優先探索を使って家系図を辿ることで、特定の先祖を見つけたり、家系全体の繋がりを理解したりすることが可能です。このように、深さ優先探索は、様々な場面で活用できる、強力な探索手法と言えるでしょう。
探索の仕組み

道を網の目のようにつないだ図を思い浮かべてください。ある地点から特定の地点への行き方を見つける方法の一つに、深さ優先探索と呼ばれるやり方があります。この方法は、例えるなら、一本道を奥深くまで進んでいくような探し方です。行き止まりにぶつかったら、少し戻って別の道を進む、ということを繰り返します。
この探し方を実現するために、入れ子になった箱のような仕組みを使います。これを「スタック」と呼びます。一番最後に箱に入れたものが、一番最初に取り出せる仕組みになっています。ちょうど、お菓子の「ポッキー」を箱から取り出す様子に似ています。
まず、出発地点をこの箱の一番上に入れます。次に、箱の一番上から地点を取り出し、そこから行ける場所を探します。まだ訪れていない場所があれば、その場所を箱の一番上に入れます。これを繰り返すことで、次々と新しい場所を探していきます。
もし行き止まりにたどり着いたら、どうなるでしょうか? 箱の一番上には、行き止まりに続く場所はありません。そこで、箱から行き止まりを取り出すと、一つ前の分岐点が現れます。そこから、まだ訪れていない別の道を探し始めることができます。
このように、スタックを使うことで、自動的に一つ前の分岐点に戻ることができるため、複雑に道が入り組んでいても、迷うことなく目的地までたどり着くことができます。深さ優先探索は、まるで迷路を解くかのように、あらゆる道をくまなく探していくことができる、効率的な探索方法なのです。
幅優先探索との違い

木構造やグラフ構造といった、 interconnected なデータ構造を探索するアルゴリズムとして、深さ優先探索と幅優先探索は広く知られています。どちらも全てのノードを漏れなく探索することを目指しますが、その進み方には大きな違いがあります。この違いを、木の探索を例に説明します。
深さ優先探索は、まるで一本道を突き進むように探索を行います。根から出発し、可能な限り深くへと進みます。枝分かれに遭遇した場合には、いずれかの枝を選び、さらに深く進みます。行き止まりに達した場合、一つ前の分岐点に戻り、まだ進んでいない別の枝を選び直します。これを繰り返すことで、まるで迷路を解くように、木の深部まで入り込んで探索を進めていきます。このため、目的とするノードが深い場所にある場合、比較的早く発見できる可能性があります。しかし、目的のノードが浅い場所にありながら、別の枝を深く探索してしまう可能性もあるため、探索範囲が広くなってしまう場合があります。
一方、幅優先探索は、根に近いノードから順に、層状に探索を進めていきます。まず根に隣接するノードを全て探索し、次にそれらのノードに隣接するノードを探索する、といった具合です。まるで池に石を投げ入れた際に、波紋が広がるように探索範囲が広がっていきます。このため、目的とするノードが浅い場所にある場合、効率的に発見できます。深さ優先探索のように、ある一つの枝を深く探索してしまうことがないため、無駄な探索を省き、最短経路で目的のノードに辿り着ける可能性が高いという利点があります。しかし、目的のノードが深い場所にある場合は、広い範囲を探索する必要が生じるため、深さ優先探索より時間がかかる可能性があります。
このように、深さ優先探索と幅優先探索はそれぞれ異なる特性を持っています。探索するデータの構造や、目的とするノードの深さなどに応じて、適切なアルゴリズムを選択することが重要です。例えば、迷路の最短経路を求める場合は幅優先探索が、家系図を辿る場合は深さ優先探索が適していると言えるでしょう。
| 項目 | 深さ優先探索 (DFS) | 幅優先探索 (BFS) |
|---|---|---|
| 探索方法 | 根から可能な限り深く探索し、行き止まりに達したら一つ前の分岐点に戻る | 根に近いノードから層状に探索する |
| 探索イメージ | 一本道を突き進む、迷路を解く | 池に石を投げ入れた時の波紋 |
| メリット | 目的のノードが深い場所にある場合、早く発見できる可能性がある | 目的のノードが浅い場所にある場合、効率的に発見でき、最短経路で見つける可能性が高い |
| デメリット | 目的のノードが浅い場所にありながら、別の枝を深く探索してしまう可能性がある | 目的のノードが深い場所にある場合、探索範囲が広くなり時間がかかる可能性がある |
| 適した例 | 家系図を辿る | 迷路の最短経路を求める |
利点と欠点

深さ優先探索は、まるで迷路を解くように、まず一つの道を可能な限り深く進んでいく探索方法です。この方法の良い点は、プログラムに組み込むのが比較的簡単だということです。複雑な手順を踏む必要がなく、単純な構造で実現できるため、初心者でも理解しやすく、手軽に利用できます。また、使用する記憶領域が少ないことも大きな利点です。一度探索した道は記憶しておく必要がないため、広大な迷路であっても、記憶容量をそれほど気にすることなく探索を進めることができます。さらに、目的の位置が迷路の奥深くにある場合、他の探索方法よりも早く見つけることができる可能性があります。まさに、一点突破で道を切り開くイメージです。
しかし、深さ優先探索にはいくつか注意すべき点もあります。例えば、迷路が非常に深い場合、探索に時間がかかってしまう可能性があります。行き止まりにぶつかるたびに、一つ前の分岐点まで戻って別の道を試す必要があるため、目的の位置によっては遠回りになってしまうこともあります。また、迷路にループが存在する場合、無限に同じ道を繰り返してしまう可能性があります。これは、まるで迷宮に迷い込んでしまったような状態で、永遠に出口を見つけられないという危険性をはらんでいます。このような事態を防ぐためには、既に通った道を記録しておくなどの工夫が必要です。一度通った道は二度と通らないようにすることで、無限ループに陥ることを防ぎ、確実に迷路を探索することができます。このように、深さ優先探索は利点と欠点を理解した上で、適切に利用することが重要です。
| 項目 | 内容 |
|---|---|
| 探索方法 | 一つの道を可能な限り深く進んでいく |
| 利点 | プログラムに組み込みやすい 記憶領域が少ない 目的が深い場合、早く見つかる可能性がある |
| 欠点 | 深い迷路だと時間がかかる 遠回りになる可能性がある ループがあると無限ループに陥る可能性がある |
| 対策 | 既に通った道を記録する |
応用例

深さ優先探索は、様々な場面で活用される、とても役立つ手法です。まるで深く伸びた枝を一本ずつ丹念に調べていくように、可能性のある道を最後まで探ってから、次の道へ移るという仕組みです。この探索方法の特徴を活かして、色々な問題を解くことができます。
例えば、迷路を考えてみましょう。行き止まりにぶつかるまで、ひたすら一つの道を進みます。行き止まりに辿り着いたら、一つ前の分岐点まで戻り、まだ進んでいない別の道を進みます。これを繰り返すことで、最終的に迷路の出口に辿り着くことができます。深さ優先探索は、まさにこの考え方で迷路を解くことができるのです。
また、鉄道や道路の経路探索にも、深さ優先探索は役立ちます。出発地から目的地までの経路を、様々な道筋を辿って探します。まず一つの経路を最後まで調べ、目的地に辿り着かない場合は、分岐点まで戻り、別の経路を探します。これを繰り返すことで、目的地までの経路を見つけ出すことができます。
ゲームの分野でも、深さ優先探索は活躍しています。例えば、囲碁や将棋などの対戦型ゲームでは、可能な手を順番に深く読み進めることで、勝利につながる手順を見つけ出すことができます。コンピュータが複雑なゲームで人間に勝つことができるのは、この深さ優先探索の力を借りているからなのです。
さらに、プログラムの翻訳にも、深さ優先探索は欠かせません。プログラムは、人間が理解しやすい言葉で書かれていますが、コンピュータが理解できる言葉に変換する必要があります。この変換作業を構文解析と言い、深さ優先探索を用いることで、プログラムの構造を正確に理解し、コンピュータが実行できる形に変換することができるのです。
このように、深さ優先探索は様々な分野で応用されています。問題解決のための基本的な道具として、これからも多くの場面で活用されていくことでしょう。
| 分野 | 深さ優先探索の活用例 |
|---|---|
| 迷路 | 行き止まりまで一つの道を進み、行き止まりに達したら一つ前の分岐点に戻って別の道を進む |
| 経路探索 | 出発地から目的地までの様々な経路を一つずつ調べ、目的地に辿り着かない場合は分岐点に戻って別の経路を探す |
| ゲーム | 囲碁や将棋で可能な手を順番に深く読み進め、勝利につながる手順を見つけ出す |
| プログラムの翻訳 | プログラムの構造を理解し、コンピュータが実行できる形に変換する構文解析に利用 |
まとめ

奥深くまで掘り下げていく探索方法である深さ優先探索は、複雑に入り組んだ構造を効率よく調べる手順です。例えるなら、迷路の中で、まず一つの道を最後まで進んで行き止まりに当たったら、一つ前の分かれ道まで戻り、別の道を進む、ということを繰り返すような方法です。
この探索方法は、行き止まりまで徹底的に調べ尽くすため、目標への道筋を見つけ出すのに役立ちます。まるで木の枝を一本ずつ辿っていくように、根元から葉の先まで、順序良く調べていくイメージです。
深さ優先探索とよく比較されるのが、幅優先探索と呼ばれる方法です。幅優先探索は、スタート地点から近い場所を全て調べてから、少し遠い場所を全て調べる、というように、層状に探索範囲を広げていく方法です。両者は、探索の進み方、必要な記憶容量、そして得意とする問題の種類が異なります。
深さ優先探索は、幅優先探索に比べて、必要な記憶容量が少ないという利点があります。これは、深さ優先探索では、現在探索中の道筋の情報だけを記憶しておけば良いからです。一方、幅優先探索では、探索済みの全ての場所を記憶しておく必要があるため、多くの記憶容量が必要となります。また、深さ優先探索は、プログラムとして組み込むのが比較的簡単であるため、様々な場面で活用されています。
例えば、ゲームにおける人工知能や、ネットワークの経路探索など、幅広い分野で応用されています。このように、深さ優先探索は、その簡潔さと効率性から、今後も様々な問題解決に役立つ重要な探索方法であり続けると考えられます。
最後に、深さ優先探索と幅優先探索は、それぞれ得意とする問題の種類が異なるため、状況に応じて適切な方法を選択することが重要です。問題の特性を理解し、どの探索方法がより効果的かを判断することで、効率的に解を求めることができます。
| 項目 | 内容 |
|---|---|
| 探索方法 | 深さ優先探索 (Depth-First Search) |
| 説明 | 奥深くまで掘り下げていく探索方法。一つの道を最後まで進んで行き止まりに当たったら、一つ前の分かれ道まで戻り、別の道を進むことを繰り返す。 |
| イメージ | 迷路、木の枝を根元から葉の先まで辿る |
| 利点 | 必要な記憶容量が少ない、プログラムとして組み込みやすい |
| 比較対象 | 幅優先探索 (Breadth-First Search) |
| 幅優先探索の説明 | スタート地点から近い場所を全て調べてから、少し遠い場所を全て調べる。層状に探索範囲を広げる。 |
| 両者の違い | 探索の進み方、必要な記憶容量、得意とする問題の種類 |
| 応用例 | ゲームにおける人工知能、ネットワークの経路探索 |
| 結論 | 問題の特性を理解し、状況に応じて適切な探索方法を選択することが重要 |
