探索を効率化!αβ法入門

AIを知りたい
先生、「αβ法」って、ゲームでAIが賢く次の手を選ぶための方法ですよね?でも、具体的にどう賢く選んでいるのかがよく分かりません。

AIエンジニア
そうだね。「αβ法」は、ミニマックス法という、自分の得点を最大化し、相手の得点を最小化する戦略に基づいた方法を効率化したもので、ゲームでAIが最善手を探すのに使われるよ。 簡単に言うと、相手にとって不利な手を探している途中で、明らかに自分にとって不利な手が見つかったら、それ以上深く探すのをやめるんだ。無駄な探索を省くことで、早く最善手を見つけられるんだよ。

AIを知りたい
なるほど。つまり、ある時点で、それ以上探しても無駄だと判断して、探索を打ち切るんですね。具体的にどういう時に打ち切るんですか?

AIエンジニア
良い質問だね。例えば、自分の番で最大の得点を探すときに、今までの最大得点よりも低い得点の手が見つかったとする。この時、その手から続く手順は、どう頑張っても今までの最大得点を超えることはないよね?だから、その時点で探索を打ち切るんだ。これをαカットと言う。逆に、相手の番で最小の得点を探す時に、今までの最小得点よりも高い得点の手が見つかったら、それ以上探す必要はない。これをβカットと言うんだ。
αβ法とは。
コンピュータの思考方法の一つである『アルファベータ法』について説明します。この方法は、ミニマックス法という、ゲームなどで一番良い手を見つける方法を効率化するために使われます。ミニマックス法では、可能なすべての手を調べて、自分にとって一番良い点と相手にとって一番悪い点を交互に比べていきます。アルファベータ法では、明らかに不利になる手は途中で探索を打ち切ることで、無駄な計算を省きます。具体的には、相手にとってより良い手が見つかった場合、それ以降の選択肢は調べなくても良いと判断する『ベータカット』と、自分にとってより悪い手が見つかった場合、それ以降の選択肢は調べなくても良いと判断する『アルファカット』という二つの工夫があります。より詳しい説明や実際に動くプログラム例は、別の資料をご覧ください。
はじめに

遊戯や謎解きをする人工知能を作る上で、探索手順の組み立て方はとても大切です。どうすれば最も良い手を見つけられるか、また、それを効率良く行うにはどうすれば良いのか、といった問いは常に探求されてきました。今回は、数ある探索手順の中でも、ミニマックス法という手順を改良した、より強力なαβ法という手順について説明します。
ミニマックス法とは、ゲームの勝ち負けを予測しながら、自分の番では最も有利な手を選び、相手の番では最も不利な手を選ぶという仮定に基づいて、最善の手を探す手順です。しかし、この手順では、全ての可能な手を調べなければならず、ゲームが複雑になるほど計算量が膨大になってしまいます。αβ法は、このミニマックス法の欠点を克服するために考案されました。
αβ法の核心は、明らかに不利な手は最後まで調べなくても良いという点にあります。具体的には、α値とβ値という二つの値を用いて、探索の範囲を絞り込みます。α値は、自分が現時点で確保できる最低限の得点を表し、β値は、相手が現時点で許容する最高限の得点を表します。探索を進める中で、ある局面における評価値がβ値を超えた場合、その局面以降の探索は不要となります。なぜなら、相手はその局面に至る前に、より有利な別の局面を選択するからです。同様に、ある局面における評価値がα値を下回った場合、その局面以降の探索も不要となります。なぜなら、自分はα値以上の得点が保証されている別の局面を選択するからです。このように、αβ法は無駄な探索を省くことで、ミニマックス法よりも効率的に最善手を見つけることができます。
αβ法は、将棋や囲碁といった複雑なゲームで、その有効性が証明されています。限られた時間の中で、より深く先を読むことができるため、高度な戦略を立てることが可能になります。人工知能の進化を支える重要な技術として、αβ法は今後も様々な分野で活躍していくことでしょう。
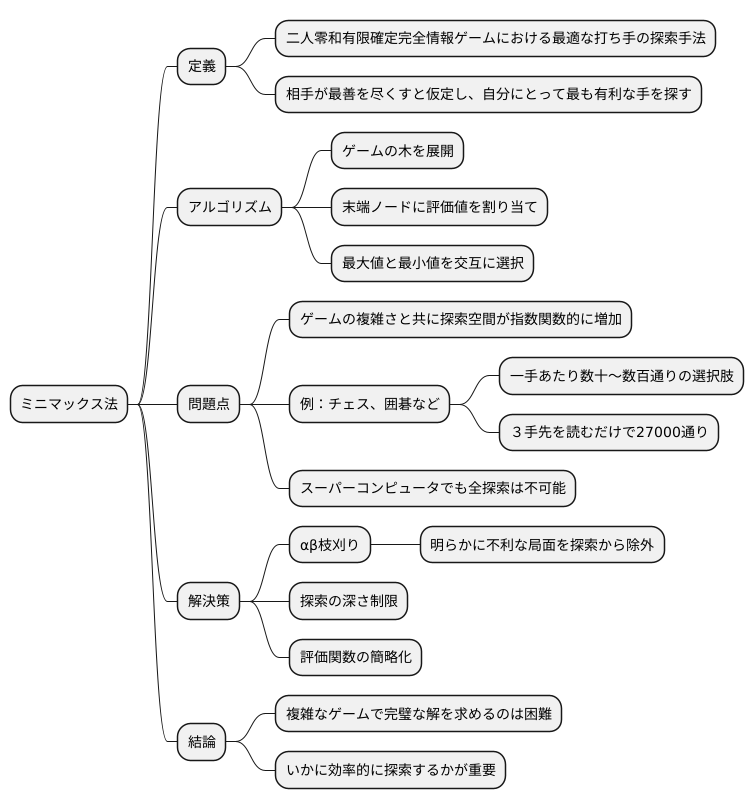
ミニマックス法の限界

ミニマックス法は、二人零和有限確定完全情報ゲームにおいて、最適な打ち手を探索するための基本的な手法です。この手法は、相手が常に最善を尽くすと仮定し、自分にとって最も有利な手を探します。具体的には、ゲームの木を展開し、末端のノードに評価値を割り当て、そこから逆向きに最大値と最小値を交互に選択することで、最適な手を見つけ出します。
しかし、ミニマックス法には大きな限界があります。それは、ゲームの複雑さが増すと、探索空間が指数関数的に増加してしまう点です。例えば、チェスや囲碁のような複雑なゲームでは、一手あたり数十から数百通りの選択肢があります。仮に一手あたり30通りの選択肢があるとすると、3手先を読むだけでも30の3乗、つまり2万7千通りもの局面を評価する必要があります。さらに深く読み進めようとすると、計算量は爆発的に増加し、現実的な時間内ではとても処理しきれません。スーパーコンピュータを用いても、すべての可能性を調べ尽くすことは不可能です。
この問題に対処するために、様々な改良が提案されています。例えば、αβ枝刈りは、明らかに不利な局面を探索から除外することで、計算量を削減する手法です。また、探索の深さを制限したり、評価関数を簡略化したりするといった工夫もよく用いられます。これらの改良により、ミニマックス法の実用性は高まりますが、それでもなお、複雑なゲームにおいて完璧な解を求めることは難しいのが現状です。限られた計算資源の中で、いかに効率的に探索を行うかが、ミニマックス法を応用する上での重要な課題となっています。
αβ法の仕組み

勝負事が好きな人は、常に最善の手を探そうとしますよね? しかし、先の手まで考えると選択肢が膨大になり、どれが良いのか分からなくなることがあります。そんな時に役立つのが、αβ法という考え方です。これは、ミニマックス法という、ゲームで最善手を見つける方法を改良したものです。
ミニマックス法は、自分が有利になる手と相手が有利になる手を交互に考え、最終的に自分が一番有利になる手を選ぶ方法です。しかし、この方法は、すべての場合を調べていくので、とても時間がかかります。そこで、αβ法は、明らかに不利になる手は調べずに、探索範囲を狭めることで、時間を短縮します。
αβ法の肝となるのが、「α値」と「β値」です。α値は、探索中に見つけた自分の手の良さの最大値を記憶します。β値は、探索中に見つけた相手の手の良さの最小値を記憶します。
たとえば、自分の番で、ある手を考えるとします。もし、その手の結果、相手が次にどんな手を打っても、自分の利益がα値よりも大きくなることが分かれば、それ以上深く考える必要はありません。なぜなら、α値以上の利益はすでに保証されているからです。これをβカットと言います。
逆に、相手の手番で、ある手を考えるとします。もし、その手の結果、自分が次にどんな手を打っても、相手の利益がβ値よりも小さくなることが分かれば、それ以上深く考える必要はありません。なぜなら、β値以下の損失はすでに保証されているからです。これをαカットと言います。
このように、αβ法は、αカットとβカットを繰り返すことで、無駄な探索を省き、効率的に最善手を見つけることができるのです。まるで、枝切りばさみで不要な枝を切るように、探索の範囲を狭めていく様子から、この名前が付けられたのかもしれませんね。
具体例で理解を深める

勝負事で最も良い手を選ぶ方法の一つに、ミニマックス法というものがあります。ミニマックス法は、可能な全ての手を調べ、相手にとって最も不利な手、つまり自分にとって最も有利な手を選ぶ方法です。しかし、この方法は、選択肢が多いと膨大な計算が必要になります。そこで、ミニマックス法を改良したαβ法が登場します。αβ法は、ミニマックス法と同じく、相手が最善手を打つと仮定して自分の最善手を探しますが、明らかに不利な手筋は探索しないことで計算量を減らす工夫がされています。
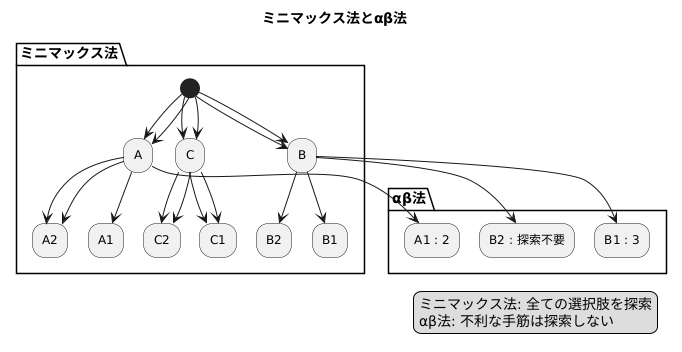
具体的に見てみましょう。先手が三つの選択肢A、B、Cを持ち、それぞれの選択肢に対して後手が二つの選択肢1、2を持つとします。ミニマックス法では、A1、A2、B1、B2、C1、C2の六通りの選択肢を全て調べなければなりません。しかし、αβ法では、場合によっては三通りで済むことがあります。
例えば、先手Aに対して後手が1と2の選択肢を持ち、後手は小さい値を選ぶとします。後手が1を選んだ場合、その値は例えば2とします。次に先手Bに対して後手が1を選んだ場合、その値が3だとします。この時、後手の2つ目の選択肢を調べる必要はありません。なぜなら、先手は大きい値を選ぶので、すでに2という値を見つけているため、3以上の値を持つB1を選ぶ可能性が高く、B2を調べるのは時間の無駄だからです。もしB2の値が1だったとしても、先手はAの2とBの3のうち3を選びます。後手は1と2のうち小さい方を選びます。
このように、αβ法は無駄な探索を省くことで、計算時間を節約します。この例は単純ですが、選択肢の数が増えれば増えるほど、αβ法の効果は大きくなります。将棋や囲碁などの複雑なゲームでは、このαβ法が重要な役割を果たしています。
プログラムで実装してみる

今回は、実際にプログラムを使って、探索アルゴリズムの一つであるαβ法を動かしてみましょう。αβ法は、ゲームなどの場面で、可能な選択肢の中から一番良い手を見つけるために使われます。この手法は、全ての手を調べることなく、明らかに不利な手は途中で切り捨てることで、計算時間を大幅に短縮できます。
αβ法は、入れ子構造になった関数を繰り返し呼び出すことで実現できます。例として、よく使われるプログラム言語の一つであるPythonで書いたプログラムを用意しました。このプログラムを実行すると、αβ法がどのように動くのかを確認できます。プログラムを一行ずつ順番に実行していくことで、αとβと呼ばれる二つの値がどのように変化し、不要な探索がどのように省かれるのかを、実際に目で見て確かめることができます。
さらに、提供されているプログラムを書き換えることも可能です。例えば、ゲームのルールを変えたり、探索の深さを変えたりすることで、様々な状況でαβ法がどのように動作するのか、自分で試して効果を実感できます。色々な条件で試すことで、αβ法の長所や短所をより深く理解できるでしょう。もちろん、Python以外のプログラム言語でも実装可能です。自分の使い慣れた言語でαβ法を実装してみるのも良いでしょう。
| 項目 | 説明 |
|---|---|
| アルゴリズム | αβ法 (探索アルゴリズム) |
| 目的 | ゲームなどの場面で、可能な選択肢の中から一番良い手を見つける。 |
| 特徴 | 明らかに不利な手は途中で切り捨てることで、計算時間を大幅に短縮。 |
| 実装方法 | 入れ子構造になった関数を繰り返し呼び出す。 |
| 例 | Pythonで書いたプログラム |
| 学習方法 |
|
まとめ

まとめとして、αβ法は、ミニマックス法が持つ欠点を克服した、より効率的な探索アルゴリズムです。ミニマックス法は、ゲームにおける最適な手を探索する際に、すべての可能性を網羅的に調べるため、計算量が膨大になりがちです。特に、ゲームの複雑さや探索の深さが増すにつれて、計算時間は指数関数的に増加し、現実的な時間内で解を求めることが困難になります。αβ法は、この問題に対処するために考案されました。
αβ法の核心は、α値とβ値を用いた枝刈りです。α値は、探索中の局面において、自分にとっての現状での最良の値を表します。一方、β値は、相手にとっての現状での最良の値を表します。探索を進める中で、これらの値を更新していきます。そして、ある局面において、β値がα値以下になった場合、その局面以降の探索は打ち切られます。なぜなら、その局面以降の探索は、自分にとってより良い結果をもたらさないことが保証されているからです。この打ち切り処理により、不要な探索を省略し、計算量を大幅に削減できます。
αβ法は、ミニマックス法と同じく、探索木を用いてゲームの状態を表現します。探索木は、根ノードが現在のゲーム状態を表し、子ノードが可能な次の状態を表します。αβ法は、この探索木を深さ優先探索で探索し、各ノードにα値とβ値を割り当てていきます。そして、枝刈りを行うことで、探索空間を狭めていきます。
αβ法は、様々なゲームに応用できる汎用的なアルゴリズムです。チェスや将棋、囲碁といったボードゲームだけでなく、ビデオゲームなどにも活用されています。また、ゲーム以外にも、探索問題を解くための一般的な手法として、人工知能の様々な分野で応用されています。αβ法を理解することは、人工知能の探索アルゴリズムを学ぶ上で重要な一歩となります。この記事で紹介された内容を参考に、さらに理解を深めていただければ幸いです。
| 項目 | 説明 |
|---|---|
| αβ法 | ミニマックス法の欠点を克服した効率的な探索アルゴリズム。不要な探索を省略することで計算量を削減。 |
| ミニマックス法の欠点 | すべての可能性を網羅的に探索するため、計算量が膨大になり、現実的な時間内で解を求めることが困難。 |
| α値 | 探索中の局面において、自分にとっての現状での最良の値。 |
| β値 | 探索中の局面において、相手にとっての現状での最良の値。 |
| 枝刈り | β値がα値以下になった場合、その局面以降の探索を打ち切る処理。 |
| 探索木 | ゲームの状態を表現する木構造。根ノードが現在の状態、子ノードが可能な次の状態を表す。αβ法は深さ優先探索で探索。 |
| 応用 | チェス、将棋、囲碁などのボードゲーム、ビデオゲーム、その他人工知能の様々な分野。 |
