αβ法:探索を効率化する賢い方法

AIを知りたい
先生、αβ法って、どういうふうに探索を減らすんでしょうか?図を見ても、よくわからないです。

AIエンジニア
そうですね、少し難しいですね。簡単に言うと、もうこれ以上探しても良い結果にならないとわかった時点で、探索を打ち切る方法です。たとえば、最小値を探している途中で、今まで見つけた最小値よりも大きな値が見つかったら、その先は探索しなくても良いですよね?

AIを知りたい
あ、確かに!それ以上探しても、最小値は更新されないですもんね。αカットとβカットの違いは何ですか?

AIエンジニア
良いところに気がつきましたね。αカットは最大値を探している時に、今まで見つけた最大値よりも小さい値が見つかった時に探索を打ち切る方法です。βカットは最小値を探している時に、今まで見つけた最小値よりも大きい値が見つかった時に探索を打ち切る方法です。つまり、αは最大値、βは最小値と覚えておけば良いですよ。
αβ法とは。
コンピュータが、例えばゲームなどで、一番良い手を探す方法の一つに、ミニマックス法というものがあります。この方法は、可能な全ての手を調べて、自分に一番有利な手を探しますが、場合によっては調べる量がとても多くなってしまいます。そこで、調べる量を減らすための工夫として「アルファベータ法」という方法があります。
この方法は、簡単に言うと、もうこれ以上良い手は見つからないと分かれば、それ以上調べないというものです。具体的には、一番低い点数を調べている途中で、既に出ている一番低い点数よりも高い点数が出てきたら、それ以降の調べを止めます。これをベータカットと言います。逆に、一番高い点数を調べている途中で、既に出ている一番高い点数よりも低い点数が出てきたら、それ以降の調べを止めます。これをアルファカットと言います。
はじめに

電算機が遊戯などで次の一手を考える際には、様々な選択肢の中から最も良い一手を見つけ出す必要があります。しかし、可能な全ての手を順々に調べていく方法(ミニマックス法と呼ばれる手法)では、場合によっては莫大な計算が必要となり、現実的ではありません。例えば、囲碁や将棋のような複雑な遊戯では、可能な手の数は天文学的数字に上ります。ミニマックス法で全ての手を調べるには、途方もない時間がかかってしまい、とても実用的とは言えません。
そこで、探索の効率を高めるための技術として、αβ法と呼ばれる手法が広く用いられています。αβ法は、ミニマックス法を改良したもので、無駄な探索を省くことで、計算量を大幅に削減し、高速な意思決定を可能にします。具体的には、ある局面における評価値が、既に探索済みの他の局面の評価値よりも悪いことが確定した場合、その局面以降の探索を打ち切ります。
αβ法は、まるで枝分かれした木を探索するように、可能な手を一つずつ調べていきます。そして、各局面での評価値を記録していきます。もし、ある枝の探索途中で、その枝の評価値が他の枝の評価値よりも明らかに悪いと判断できれば、その枝の探索を途中で打ち切っても構いません。なぜなら、その枝の先にある局面がどんなに良くても、他の枝の評価値を超えることはないからです。
このように、無駄な探索を省くことで、αβ法はミニマックス法に比べてはるかに少ない計算量で最善の一手を見つけることができます。この手法は、遊戯人工知能をはじめ、様々な計画立案や意思決定が必要な分野で応用されています。例えば、ロボットの行動計画や、資源配分問題などにも利用されています。αβ法は、限られた時間の中で効率的に最善の行動を選択する必要がある場面で、非常に強力な道具となるのです。
ミニマックス法の限界

勝負事が得意な計算機を作るには、先を読むことが大切です。ミニマックス法は、このような計算機を実現するためによく使われる方法です。まるで木の枝のように、可能な手順を一つ一つ書き出し、それぞれの良し悪しを数値で評価することで、一番良い手を探し出します。
しかし、この方法は、ゲームが複雑になるほど、限界が見えてきます。例えば、将棋や囲碁を考えてみましょう。一手ごとにたくさんの選択肢があり、その後の手順も考えると、枝分かれは爆発的に増えます。この枝分かれ全体を「ゲーム木」と呼びますが、将棋や囲碁のような複雑なゲームでは、このゲーム木がとてつもなく巨大になります。全ての枝を一つ一つ計算していくのは、途方もない時間がかかり、現在の計算機の能力では現実的ではありません。
ミニマックス法の限界は、この計算量の多さにあります。たとえすごく速い計算機を使ったとしても、あまりに選択肢が多いと、すべての可能性を調べつくす前に時間が過ぎてしまいます。特に、一手ごとにたくさんの選択肢があるゲームや、何十手も先まで読まなければならないゲームでは、この問題は深刻です。
そこで、ミニマックス法を改良した方法が考え出されてきました。例えば、明らかに不利な手順は途中で切り捨てることで、計算量を減らす工夫などです。αβ法もそのような工夫の一つで、無駄な計算を省くことで、ミニマックス法の限界を少しでも克服しようとしています。複雑なゲームで、限られた時間の中でより良い手を導き出すためには、このような工夫が欠かせません。

αβ法の仕組み

二人零和有限確定完全情報ゲームにおける探索アルゴリズムであるαβ法は、ミニマックス法が持つ問題点を解決する手法です。ミニマックス法は、ゲーム木を全て探索するため、計算量が膨大になりがちです。そこで、αβ法は、明らかに最善手にならない部分を探索せずに済むよう、枝刈りを行います。この枝刈りによって、ミニマックス法と同じ結果を得つつ、計算コストを大幅に削減できます。
αβ法では、α値とβ値という二つの値を用いて探索範囲を絞り込みます。α値は、探索中の経路で見つかった最大値を保持し、β値は最小値を保持します。これらの値は、探索木を上から下へと降りていく過程で更新されていきます。
具体的には、先手番は、子ノードの中で最大の評価値を選択しようとします。この時、子ノードの評価値がβ値以上になった場合、そのノード以下の探索は打ち切られます。なぜなら、後手番はβ値以下の値を選択することができ、先手番にとってそれ以上の探索は意味がないからです。
逆に、後手番は、子ノードの中で最小の評価値を選択しようとします。この時、子ノードの評価値がα値以下になった場合、そのノード以下の探索は打ち切られます。なぜなら、先手番はα値以上の値を選択することができ、後手番にとってそれ以上の探索は意味がないからです。
このように、α値とβ値を巧みに利用することで、無駄な探索を省き、効率的に最善手を探すことが可能になります。αβ法は、チェスや将棋、囲碁といった様々なゲームで使用されており、ゲームAI開発において重要な技術となっています。
αカットとβカット

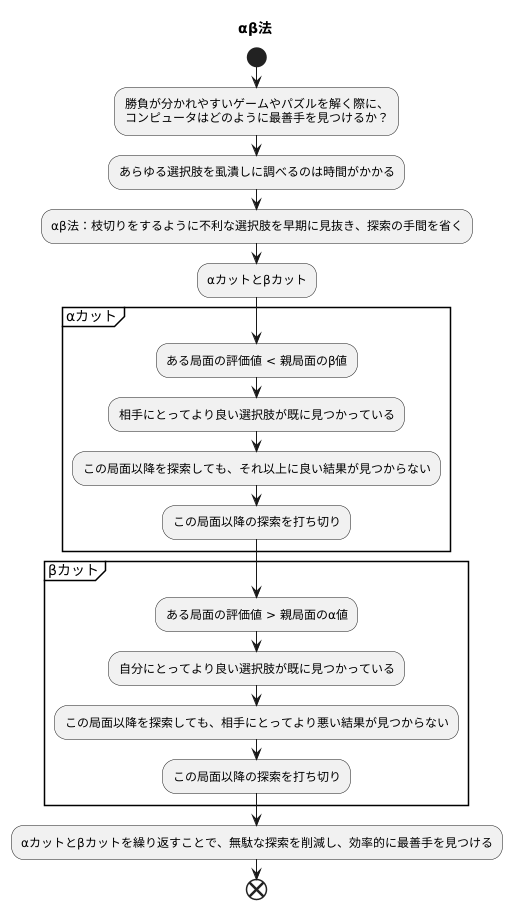
勝負が分かれやすいゲームやパズルを解く際に、コンピュータはどのようにして最善手を見つけるのでしょうか? 多くの場合、あらゆる選択肢を虱潰しに調べるのは、あまりに時間がかかります。そこで登場するのが「αβ法」と呼ばれる技術です。αβ法は、まるで枝切りをするように、明らかに不利な選択肢を早期に見抜いて、探索の手間を省く方法です。この枝切りに用いられるのが、「αカット」と「βカット」です。
αβ法では、まず、自分の番であれば最大の利益、相手の番であれば最小の損失となるように手を探します。この時、各局面に点数をつけ、その局面の良し悪しを評価します。この探索の過程で、α値とβ値という二つの重要な値を用います。α値は、現時点でその局面に至るまでの経路で見つかった、自分にとっての最低保証の点数です。一方、β値は相手にとっての最大損失、つまり自分にとっての最高期待値です。
αカットは、ある局面の評価値が、その親局面のβ値よりも小さくなった時に起こります。 これは、相手にとってより良い選択肢が既に見つかっているため、この局面以降を探索しても、それ以上に良い結果が見つかることはない、ということを意味します。そこで、この局面以降の探索は打ち切られます。例えるなら、対戦相手が既に強力な一手を発見しているのに、それより弱い手を探し続ける必要はない、ということです。
一方、βカットは、ある局面の評価値が、その親局面のα値よりも大きくなった時に起こります。これは、自分にとってより良い選択肢が既に見つかっていることを意味し、この局面以降を探索しても、相手にとってより悪い結果が見つかることはない、ということです。よって、この局面以降の探索は打ち切られます。これは、自分が既に良い手を見つけているのに、相手にとって更に都合の良い手をわざわざ探しに行く必要はない、という状況に例えられます。
このように、αカットとβカットを繰り返すことで、無駄な探索を大幅に削減し、効率的に最善手を見つけることができます。 まるで熟練の職人が無駄な動きを一切せずに、最短距離で目的を達成するように、αβ法はコンピュータに知的な探索能力を与えているのです。
αβ法の効果

αβ法は、ゲームなどでよく使われる、コンピューターが最善の手を考えるための方法です。 簡単に言うと、先を読むことで、自分にとって一番良い手、相手にとって一番悪い手を交互に見つけていきます。この時、すべての可能性をくまなく調べるのは大変なので、αβ法は賢い工夫で調べる量を減らします。
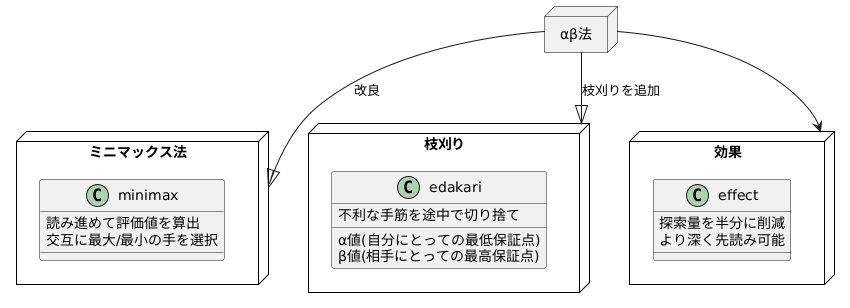
αβ法は、ミニマックス法という基本的な方法を改良したものです。ミニマックス法では、可能な限り先まで読み進め、その先で得られる点数を評価します。そして、自分の番では点数が最大になる手を選び、相手の番では点数が最小になる手を選びます。これを交互に繰り返すことで、最善の手を探します。αβ法は、このミニマックス法に、枝刈りという仕組みを追加します。
枝刈りとは、明らかに不利な手筋を、最後まで調べずに途中で切り捨てることです。 例えば、自分の番で、ある手筋を調べた結果、点数が50点だったとします。次に別の筋を調べ始めたところ、途中で相手が必ず30点以下にできることが分かりました。この場合、この筋を最後まで調べても、50点より良い結果にはなりません。なので、この筋の続きを調べるのは無駄なので、途中でやめます。これが枝刈りです。
αβ法では、α値とβ値という2つの値を使います。α値は、これまでに調べた中で、自分にとっての最低保証点です。β値は、これまでに調べた中で、相手にとっての最高保証点です。探索を進める中で、これらの値を更新していきます。そして、ある筋を調べている途中で、その筋の点数がβ値より小さくなることが分かったら、その筋の探索を打ち切ります。逆に、α値より大きくなることが分かったら、相手の番なので、その筋の探索を打ち切ります。
αβ法を使うことで、ミニマックス法に比べて、同じ深さまで先読みした場合、調べる量を半分程度に減らせると言われています。つまり、より短い時間で、より深く先読みできるようになり、より強いコンピューターを作ることができます。
適用事例

勝負を決める手順を考える場面でよく使われる方法に、αβ法というものがあります。これは、ゲームの対戦相手の手を想定しながら、自分の勝利に繋がる手順を効率的に探す方法です。
例えば、将棋や囲碁、チェス、オセロといった、様々な手順があり得る盤面ゲームを考えてみましょう。これらのゲームでは、可能な手順の数が非常に多く、全ての手順を一つ一つ検討するのは現実的ではありません。そこで、αβ法を用いることで、無駄な手順の検討を省き、勝利に繋がる手順だけを効率的に絞り込むことができます。
αβ法は、相手の手も予想しながら、自分の最善手を探します。具体的には、まず自分の可能な手順を全て検討し、それぞれの手順による評価値を計算します。この評価値は、その手順がどれくらい有利かを表す数値です。そして、相手の手番になった時、相手は自分の評価値を最小にするような手順を選ぶと仮定します。つまり、相手は自分の不利になるような手順を選ぶと考えます。
この時、α値とβ値という二つの値を用いて、探索範囲を絞り込みます。α値は、これまでに探索した手順の中で、自分にとっての最低保証されている評価値を表します。β値は、これまでに探索した手順の中で、相手にとっての最高保証されている評価値を表します。
探索を進めていく中で、ある手順の評価値がβ値よりも小さい場合、その手順以降の探索は行いません。なぜなら、相手はその手順を選ばないからです。同様に、ある手順の評価値がα値よりも大きい場合、そのα値を更新します。
αβ法は、ゲーム以外にも様々な分野で応用されています。例えば、目的地までの最短経路を探す場合や、工場などで機械を動かす手順を決める場合、商品の売買を自動で行う場合などにも、αβ法の考え方が利用されています。αβ法は、複雑な問題を効率的に解くための、強力な道具と言えるでしょう。
| 項目 | 説明 |
|---|---|
| αβ法 | ゲームの対戦相手の手を想定しながら、自分の勝利に繋がる手順を効率的に探す方法 |
| 適用例 | 将棋、囲碁、チェス、オセロなど |
| 評価値 | 手順の有利さを表す数値 |
| 相手の仮定 | 自分の評価値を最小にする手順を選ぶ |
| α値 | 探索済みの手順の中で、自分にとっての最低保証評価値 |
| β値 | 探索済みの手順の中で、相手にとっての最高保証評価値 |
| 探索範囲の絞り込み | 評価値がβ値より小さい場合、その手順以降の探索を打ち切る。評価値がα値より大きい場合、α値を更新。 |
| αβ法の応用 | 最短経路探索、機械の動作手順決定、商品の売買など |
