大域最適解とは?:本当の最適解を求めて

AIを知りたい
先生、「大域最適解」って一体何ですか?難しそうでよくわからないです。

AIエンジニア
そうだね、少し難しいかもしれないね。例えて言うと、広い山脈の中で一番低い谷底を探すようなものだよ。この一番低い谷底が「大域最適解」にあたるんだ。AIは学習を通して、この一番低い谷底を目指して進んでいくんだよ。

AIを知りたい
なるほど。じゃあ、他の谷底もあるんですか?

AIエンジニア
そうだよ。他の谷底もあるんだけど、それは一番低い谷底ではないから「局所最適解」と呼ばれるんだ。一番低い谷底(大域最適解)を見つけるためには、学習の歩幅を大きくしたり、様々な工夫が必要になるんだよ。
大域最適解とは。
人工知能の話でよく出てくる『一番いい答え』について説明します。この『一番いい答え』というのは、機械学習のやり方の一つである勾配降下法で、本当に一番いい答えのことを指します。この一番いい答えを見つけるためには、学習の進み具合を調整するなど、いくつか工夫が必要になります。
最適解の種類

何かをより良くしたい、という思いは人間の持つ普遍的な欲求の一つと言えるでしょう。より良い結果を求めて試行錯誤する中で、私たちはしばしば「最適化」という問題に直面します。最適化とは、様々な制約条件のもとで、最も良い結果を見つけ出すことです。例えば、限られた予算で最大の効果を得る広告戦略を立てる、限られた時間の中で最も多くの仕事をこなす、といったことが挙げられます。このような最適化問題を解く際に重要なのが、「最適解」の概念です。最適解とは、与えられた条件下で最も良い結果のことです。
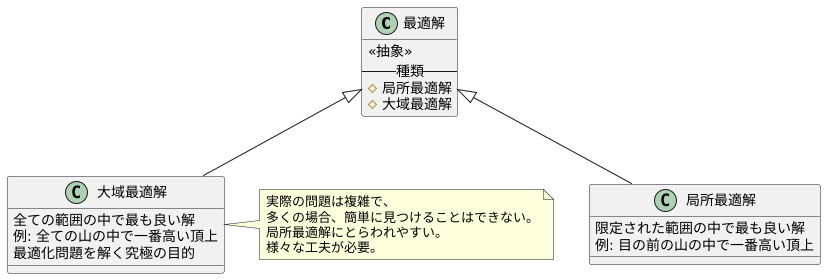
最適解には、大きく分けて二つの種類があります。一つは「局所最適解」、もう一つは「大域最適解」です。局所最適解とは、限定された範囲の中で最も良い解のことです。例えば、目の前にあるいくつかの山の中で、一番高い山の頂上が局所最適解です。しかし、さらに遠くにもっと高い山があるかもしれません。局所最適解は、あくまでも目の前の範囲で最も良い解に過ぎないのです。
一方、大域最適解とは、全ての範囲の中で最も良い解のことです。全ての山の中で一番高い山の頂上が大域最適解に当たります。最適化問題を解く究極の目的は、この大域最適解を見つけることです。しかし、実際の問題は複雑で、多くの場合、簡単に大域最適解を見つけることはできません。特に複雑な問題では、局所最適解にとらわれてしまい、真の最適解である大域最適解にたどり着けないことがしばしばあります。まるで、目の前の山の頂上に満足してしまい、より高い山があることに気づかないようなものです。
そのため、大域最適解を見つけるためには、様々な工夫が必要です。局所最適解にとらわれずに、より広い範囲を探索する必要があります。様々な探索方法を組み合わせたり、問題の性質を深く理解することで、真に最適な解を見つけ出すことができるでしょう。
勾配降下法と大域最適解

勾配降下法は、機械学習の分野で最適な解を見つけるためによく使われる手法です。この方法は、いわば山の頂上から麓へ降りる道筋を探すようなものです。山の斜面の傾きが急な方向へ進むことで、徐々に低い場所へと移動していきます。この傾きに当たるのが、関数の勾配です。勾配降下法は、この勾配情報を利用して、目的とする関数の値が最も小さくなる点、すなわち最適解を探し出します。
しかし、この方法には落とし穴があります。山には大小様々な谷が存在する様に、関数にも複数の極小点が存在する可能性があります。勾配降下法は、常に最も近い谷底に向かって進んでいくため、必ずしも一番深い谷底、つまり大域最適解にたどり着くとは限りません。近くの小さな谷底で立ち往生してしまうと、全体で見れば最適とは言えない局所最適解に留まってしまいます。これは、麓を目指して下山する際に、近くの小さな谷に降りてしまい、一番深い谷底にたどり着けないことに例えられます。
大域最適解を見つけるためには、いくつかの工夫が必要です。その一つが学習率の調整です。学習率とは、山の斜面を下る際の「一歩の大きさ」を指します。一歩が大きすぎると、最適解を通り過ぎてしまい、麓にたどり着けません。逆に一歩が小さすぎると、なかなか麓にたどり着かず、局所最適解から抜け出せなくなってしまいます。そのため、適切な一歩の大きさ、つまり適切な学習率を設定することが非常に重要です。また、異なる初期値から探索を開始するのも有効な方法です。山の頂上ではなく、様々な中腹から下山を開始することで、より深い谷底を見つけられる可能性が高まります。複数の出発点から探索を行うことで、局所最適解に囚われずに、真の大域最適解に近づく可能性を高めることができます。
大域最適解への挑戦

あらゆる問題において、最も良い答え、つまり大域最適解を見つけることは容易ではありません。特に、問題が複雑で、様々な制約条件が存在する場合、最適解を見つけることは大きな挑戦となります。山や谷が複雑に入り組んだ地形を想像してみてください。それぞれの谷底が局所最適解であり、最も深い谷底が大域最適解に相当します。単純な探索方法では、近くの谷底に降りて満足してしまい、最も深い谷底、つまり真の最適解を見逃してしまう可能性があります。
例えば、勾配降下法という手法は、現在地から最も急な坂道を下るように探索を進めます。この方法は、単純で計算コストも低いという利点がありますが、最初に降り立った谷底が最も深い谷底とは限らないという問題を抱えています。つまり、局所最適解に捕まってしまい、大域最適解に到達できない可能性があるのです。
このような問題を克服するために、より高度な探索手法が開発されています。遺伝的アルゴリズムは、生物の進化を模倣した手法で、複数の探索点を同時に動かし、良い探索点の特徴を組み合わせることで、より良い解を探索します。また、焼きなまし法は、あえて一時的に悪い方向へ探索を進めることで、局所最適解から抜け出し、より良い解を探索する手法です。これらの手法は、計算コストは高くなりますが、複雑な問題において大域最適解を見つける可能性を高めます。
最適な解を見つけるためには、問題の性質を理解し、適切な手法を選択することが重要です。単純な問題であれば、単純な手法で十分な場合もありますし、複雑な問題であれば、高度な手法が必要となる場合もあります。また、計算時間や利用可能な資源も考慮に入れて、最適な手法を選択する必要があります。最適解を求める旅は、まさに挑戦の連続であり、様々な工夫と試行錯誤が必要となるのです。
| 手法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 勾配降下法 | 現在地から最も急な坂道を下るように探索を進める | 単純、計算コストが低い | 局所最適解に捕まりやすい |
| 遺伝的アルゴリズム | 生物の進化を模倣し、複数の探索点を同時に動かし、良い探索点の特徴を組み合わせることで、より良い解を探索する | 複雑な問題において大域最適解を見つける可能性を高める | 計算コストが高い |
| 焼きなまし法 | あえて一時的に悪い方向へ探索を進めることで、局所最適解から抜け出し、より良い解を探索する | 複雑な問題において大域最適解を見つける可能性を高める | 計算コストが高い |
学習率の調整方法

機械学習において、学習の進み具合を調整する学習率は、目的とする最適な結果を得る上で非常に重要な役割を果たします。この学習率の設定が適切でない場合、様々な問題が発生する可能性があります。
まず、学習率の設定値が大きすぎる場合を考えてみましょう。学習率が大きいということは、一度の学習で大きく変化することを意味します。これは、最適な値を通り過ぎてしまい、値が振動してしまう状況を引き起こします。まるで目的地へ行く途中で、行き過ぎてしまい、何度も前後に通り過ぎてしまうようなものです。結果として、最適な値に落ち着くことができず、学習がうまく進みません。
逆に、学習率の設定値が小さすぎる場合、最適な値に近づくための一歩が小さすぎることになります。これは、目的地まで非常に時間がかかることを意味します。さらに、最適な値ではないものの、一見最適に見える値で学習が止まってしまう可能性があります。これは、真の目的地ではなく、途中の休憩所で満足してしまうようなものです。結果として、最適な値にたどり着くまでに長い時間がかかるだけでなく、本当に最適な値を見つけることができない可能性があります。
最適な学習率は、扱う問題やデータの量によって異なります。そのため、様々な値を試す必要があります。一般的には、最初は大きな値から始め、徐々に小さな値へと調整していく方法が用いられます。また、学習の進み具合を見ながら、学習率を自動的に調整する方法もあります。適切な学習率を見つけることで、最適な結果により早くたどり着くことができます。
| 学習率 | 状態 | 結果 | 例え |
|---|---|---|---|
| 大きすぎる | 値が振動し、最適な値に落ち着かない | 学習がうまく進まない | 目的地を行き過ぎて何度も前後に通り過ぎる |
| 小さすぎる | 最適な値に近づくのが遅く、局所解に陥る可能性がある | 最適な値にたどり着くまでに時間がかかり、真の最適値を見つけられない可能性がある | 途中の休憩所で満足してしまう |
様々な最適化手法

最適な解を見つけるための方法は、下り坂を進むように探す方法以外にもたくさんあります。様々な方法があり、それぞれに特徴があります。まず、勢いをつけるように探す方法を考えてみましょう。これは、以前の下り坂の情報を覚えておき、それを参考にしながら進む方法です。まるでボールが坂を転がるように、勢いを増しながら最適な解へと近づいていきます。この方法を使うと、単純な下り坂を進む方法よりも早く最適な解にたどり着けることがあります。
次に、勢いをつける方法と揺れを抑える方法を組み合わせた方法があります。この方法は、学習の速さを自動的に調整する機能も持っています。例えるなら、自転車に乗ることを想像してみてください。坂道を下るときはスピードを上げ、上り坂ではスピードを落とすように、状況に合わせて最適な速さで進みます。この方法により、より効率的に最適な解を探すことができます。
さらに、下り坂の曲がり具合まで考慮する方法もあります。これは、より精密な情報を使って最適な解へと進む方法です。そして、この方法を少し簡略化した方法もあります。これらの方法は、下り坂を進む方法よりも速く最適な解にたどり着ける場合が多いですが、計算に時間がかかる傾向があります。
このように、最適な解を見つけるための方法は様々です。どの方法が最適かは、問題の種類や使える計算資源によって異なります。例えば、複雑な問題では精密な方法が必要ですが、計算資源が少ない場合は、簡単な方法を選ばなければなりません。適切な方法を選ぶことで、より効率的に最適な解を見つけることができます。
| 方法 | 説明 | 特徴 |
|---|---|---|
| 下り坂を進む方法 | 単純に下り坂を進む | 基本的な方法 |
| 勢いをつける方法 | 以前の下り坂の情報を参考に進む | 下り坂を進む方法より速い場合がある |
| 勢いをつける方法 + 揺れを抑える方法 | 学習の速さを自動調整 | 自転車のように状況に合わせて速度調整 |
| 下り坂の曲がり具合まで考慮する方法 | 精密な情報を使って進む | 速いが計算に時間かかる |
| 下り坂の曲がり具合まで考慮する方法(簡略化版) | 上記を簡略化 | 速いが計算に時間かかる |
初期値の影響

最適化の計算では、最初の値の設定が最終的な結果に大きく影響します。最初の値が適切でないと、局所最適解と呼ばれる、全体で見れば最適ではない解に捕まってしまうことがあります。ちょうど、山の頂上を探している登山家が、近くの小さな丘の頂上で満足してしまい、真の最高峰に辿り着けないようなものです。最初の値がたまたま真の最適解に近い場合は、スムーズに最適解を見つけることができますが、最適解の位置は事前にわからないため、最初の値をどのように設定するかは難しい問題です。
この問題に対処するためには、様々な異なる最初の値から計算を始めることが重要です。複数の異なる地点から登山を開始し、それぞれの結果を比較することで、真の最高峰を見つけ出す可能性が高まります。最初の値をランダムに設定する方法や、データの性質に基づいて設定する方法など、様々な手法があります。例えば、データの平均値や中央値を最初の値として利用する、データの分布範囲を考慮して複数の値を均等に配置する、といった方法が考えられます。
計算に利用できる資源(時間や計算能力)も考慮する必要があります。最初の値を多く設定すれば最適解を見つける可能性は高まりますが、その分計算量も増えます。限られた資源の中で効率的に最適解を探すためには、最初の値の設定方法と計算量のバランスを考える必要があります。また、問題の種類によっては、特定の性質を持つ最初の値を設定することで計算の効率を上げられる場合があります。それぞれの最適化問題に適した最初の値の設定方法を見つけることが、最適解への近道と言えるでしょう。
| 問題点 | 対処法 | 具体的な手法 | 考慮事項 |
|---|---|---|---|
| 最初の値の設定が最終結果に大きく影響し、局所最適解に捕まる可能性がある。 | 様々な異なる最初の値から計算を始める。 | ・ランダムに設定 ・データの平均値や中央値を利用 ・データの分布範囲を考慮して均等に配置 |
・計算資源(時間、計算能力) ・最初の値の設定方法と計算量のバランス ・問題の種類に適した設定方法 |
