誤差逆伝播法：学習の仕組み

誤差逆伝播法：学習の仕組み

はじめに

人間の頭脳の働きを真似て作られた仕組み、人工知能。中でも、深層学習という分野で活躍しているのが、ニューラルネットワークです。これは、人間の脳の神経細胞の繋がりを模したモデルで、様々な情報を学習し、処理することができます。このニューラルネットワークを上手に学習させるための大切な方法の一つが、誤差逆伝播法です。

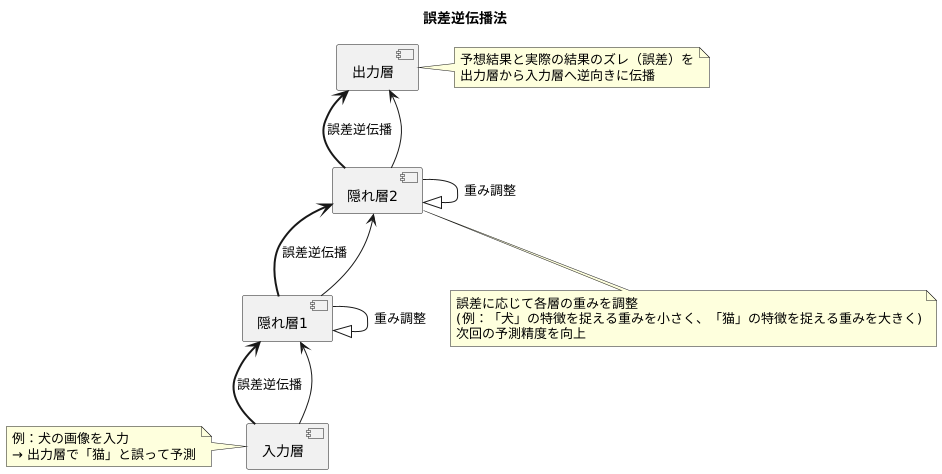
誤差逆伝播法とは、簡単に言うと、予想した結果と実際の結果のズレを、ネットワーク全体に逆方向へ伝えることで、学習を進める方法です。例えば、画像を見て「猫」と判断する人工知能を想像してみてください。もし、犬の画像を見て「猫」と答えてしまったら、それは間違いです。この間違い、つまり予想と現実のズレを「誤差」と呼びます。この誤差を、出力層から入力層へ、逆向きに伝えていきます。

この時、それぞれの神経細胞の繋がり具合（重み）を、誤差に応じて少しずつ調整していきます。「猫」と答えるべきところで「犬」と答えてしまった場合、「犬」の特徴を捉える部分の重みを小さくし、「猫」の特徴を捉える部分の重みを大きくすることで、次回の予測精度を向上させるのです。このように、誤差を逆向きに伝えることで、ネットワーク全体が徐々に正しい答えを出せるように学習していくのです。

この誤差逆伝播法は、特に複雑な構造を持つ多層ニューラルネットワークの学習に不可欠です。層が深くなるほど、単純な方法では学習が難しくなりますが、誤差逆伝播法を用いることで、それぞれの層の重みを適切に調整し、全体として精度を高めることができます。このおかげで、深層学習は大きく発展し、画像認識や音声認識など、様々な分野で目覚ましい成果を上げています。まさに、誤差逆伝播法は、現代の人工知能技術を支える重要な柱の一つと言えるでしょう。

多層構造と重み

人間の脳の神経細胞の仕組みを模倣したものが、人工知能の中核技術であるニューラルネットワークです。これは、幾つもの層が重なり合う多層構造を成しています。層には大きく分けて三つの種類があります。情報の入り口となる入力層、情報を処理する中間層（隠れ層）、そして最終的な結果を送り出す出力層です。

それぞれの層は、たくさんの小さな処理単位であるノード（ニューロン）が繋がってできています。このノード同士を繋ぐのが、重みと呼ばれる数値です。入力された情報は、この重みを掛け合わされることで、次の層へと伝達されていきます。重みは、いわば情報の重要度を決める役割を担っています。例えば、ある画像に含まれる特徴のうち、猫の耳の形が重要な情報であれば、その部分に繋がる重みの値は大きくなります。逆に、背景の模様などは重要度が低いため、重みの値は小さくなります。

ニューラルネットワークの層の数を増やす、つまり多層化することで、より複雑な事柄を学習できるようになります。例えば、単純な直線や曲線だけでなく、猫の顔全体といった複雑な形も認識できるようになります。これは、層が増えるごとに、様々な特徴を段階的に抽出できるようになるためです。しかし、層の数が増えるとともに、調整すべき重みの数も増えていきます。重みの数が多すぎると、学習に時間がかかったり、うまく学習できないといった問題が起こることがあります。そのため、この重みをどのように調整していくかが、ニューラルネットワークの学習における重要な課題となります。適切に調整された重みを持つニューラルネットワークは、高精度な予測や判断を行うことができます。

誤差の計算

誤差の計算は、学習を繰り返して予測の正確さを高めるために欠かせません。この計算は、予測値と実際の値との差を見ることで行われます。この差が誤差と呼ばれ、モデルの正確さを示す大切な指標となります。誤差が小さければ小さいほど、モデルの予測は正確だと言えます。

具体的には、まずモデルにデータを入力し、予測値を得ます。次に、この予測値と、実際の値を比較します。例えば、画像に写っているものが「猫」であると予測したのに、実際は「犬」だった場合、これは誤差となります。この誤差を数値化することで、モデルがどの程度正確に予測できているかを測ることができます。

誤差を計算するための方法は様々ですが、よく使われるのが損失関数を用いる方法です。損失関数は、予測値と実際の値の差を計算するための計算式です。損失関数の種類はたくさんあり、扱うデータの種類や予測したい内容に合わせて適切なものを選ぶ必要があります。例えば、分類問題では交差エントロピー誤差関数、回帰問題では平均二乗誤差関数がよく使われます。

このように、誤差を計算し、その値を小さくするようにモデルを調整していくことで、より正確な予測ができるようになります。誤差逆伝播法はこの調整方法の一つで、誤差を基にモデルの各部分を修正していくことで、全体の予測精度を高めることができます。適切な損失関数を選び、誤差を効果的に利用することで、モデルの性能を最大限に引き出すことが可能になります。

誤差の逆伝播

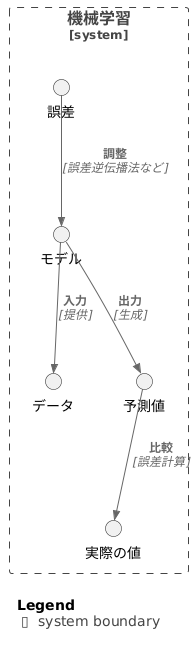
誤差の逆伝播とは、人工知能の学習方法である機械学習、特に深層学習で使われる大切な考え方です。 これは、人工知能が予想した答えと本当の答えとの違いである「誤差」を、出力層から入力層へと逆向きに伝えることで、人工知能の性能を向上させる方法です。 ちょうど、ボールを投げたときに的を外した場合、その投げ方を修正するために、どのような投げ方をすれば良かったのかを振り返るようなものです。

人工知能は、たくさんの層が重なってできており、それぞれの層にはたくさんの「重み」と呼ばれる数値が設定されています。 これらの重みは、入力された情報を次の層に伝える際に、情報の重要度を調整する役割を果たします。 誤差の逆伝播では、各層の重みが誤差にどの程度影響を与えているかを計算します。 この計算は、連鎖律と呼ばれる微分の法則を用いて行われます。 連鎖律とは、複雑な関数の微分を、その関数を構成する単純な関数の微分の積として計算できるという法則です。 誤差の逆伝播では、この連鎖律を用いることで、複雑なネットワークにおける各重みの誤差への影響度を効率的に計算することができます。

計算された影響度に基づいて、重みを調整することで、人工知能は次回の予想で誤差を小さくするように学習します。 つまり、重みの調整は、投げ方の修正にあたります。 この繰り返しによって、人工知能は次第に精度を高めていきます。 誤差の逆伝播は、現在の深層学習において非常に重要な役割を果たしており、画像認識や音声認識など、様々な分野で活用されています。

このように、誤差の逆伝播は、人工知能が学習する上で欠かせない手法であり、その仕組みを理解することは、人工知能の学習プロセスを理解する上で非常に重要です。

重みの更新

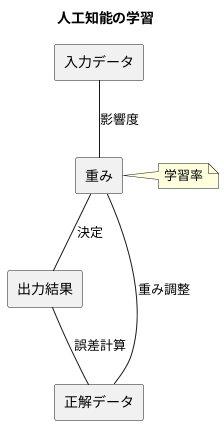
学習とは、人工知能が与えられたデータからパターンや規則を学ぶ過程です。この学習過程で重要な役割を担うのが、重みと呼ばれる数値です。重みは、入力データがどの程度出力に影響するかを表す指標であり、適切な重みを設定することで、人工知能は正確な予測や判断を行うことができます。

人工知能の学習は、試行錯誤の繰り返しです。まず、初期状態では重みはランダムに設定されます。次に、入力データを与え、その出力結果と正解データとの誤差を計算します。この誤差を基に、重みを調整することで、より正確な出力結果を得られるように学習を進めます。

重みの調整方法として、勾配降下法という手法がよく用いられます。勾配降下法は、山の斜面を下るように、誤差が小さくなる方向に重みを少しずつ調整していく方法です。具体的には、誤差の大きさを示す指標を計算し、その指標が小さくなるように重みを更新します。この際、一度にどれだけの量を更新するかは、学習率という数値で調整します。

学習率は、学習の速度を左右する重要な要素です。学習率が大きすぎると、最適な重みを通り過ぎてしまい、学習が不安定になる可能性があります。逆に、学習率が小さすぎると、学習に時間がかかりすぎるという問題が生じます。そのため、最適な学習率は、試行錯誤によって慎重に決定する必要があります。適切な学習率を設定することで、人工知能は効率的に学習を進め、高精度な予測や判断を行うことができるようになります。

学習の繰り返し

人工知能の学習は、ちょうど子供が何度も繰り返し練習することで新しいことを覚える過程によく似ています。この学習の核となる部分は、大きく分けて三つの段階に分けることができます。まず、現在の状態での人工知能の予測と、実際の正解との間の違いを計算します。この違いのことを誤差と呼びます。まるで子供が描いた絵と、お手本の絵を比べて、どこが違うのかを確認するようなものです。

次に、この誤差を基に、人工知能の内部構造である重みを調整します。これは、子供が絵を描く際に、うまくいかなかった部分を修正するように、人工知能が自身の予測を改善するための調整を行う過程です。具体的には、誤差が小さくなる方向に重みを少しずつ変化させます。この過程は逆伝播と呼ばれ、誤差を基に、どの部分をどのように修正すれば良いのかを計算する重要なステップです。

そして最後に、修正された重みを元に、再度予測を行います。この一連の流れ、つまり誤差の計算、重みの調整、そして再予測という三つの段階を繰り返し行うことで、人工知能は徐々に学習し、より正確な予測ができるようになります。この繰り返しの回数のことをエポックと呼びます。エポック数を適切に設定することは、人工知能の学習において非常に重要です。

もし、エポック数が少なすぎると、人工知能は十分に学習できず、予測精度が低くなってしまいます。逆に、エポック数が多すぎると、過学習と呼ばれる状態に陥ることがあります。これは、子供が練習問題を完璧に解けるようになっても、応用問題が解けない状態に似ています。つまり、学習に用いたデータに特化しすぎてしまい、新しいデータに対してはうまく対応できないという状態です。

そのため、学習の進捗状況を誤差の変化や精度といった指標で常に監視し、適切なエポック数を見つける必要があります。適切なエポック数で学習を止めることで、過学習を防ぎ、様々な状況に対応できる汎化性能の高い人工知能を構築することが可能になります。