分割統治法:問題解決への近道

AIを知りたい
先生、『分割統治法』って、AIの世界ではどんな時に使うんですか? 大きな問題を小さく分けて考えるっていうのは、なんとなくわかるんですけど…

AIエンジニア
いい質問だね。たとえば、すごく複雑なゲームを考えてみよう。将棋とかチェスのようなゲームは、一手一手は単純だけど、全部の組み合わせを考えると膨大な量になるよね。こんな時に、分割統治法が役立つんだ。

AIを知りたい
なるほど。でも、どうやって分けて考えるんですか?

AIエンジニア
ゲームをいくつかの局面に分割していくんだ。そして、それぞれの局面でどうなるかを考えて、一番良い手を選ぶ。AIは先の先まで読むから、この分割統治法を使うことで、全部を考えなくても、効率的に良い手を見つけられるんだよ。
分割統治法とは。
人工知能の分野でよく使われる『分割統治法』について説明します。分割統治法とは、複雑で大きな問題を、扱いやすい小さな問題に分割し、それぞれの小さな問題を解いていく方法です。すべての小さな問題が解決したら、それらを組み合わせて、元の大きな問題の解決策を得ます。
分割統治法とは

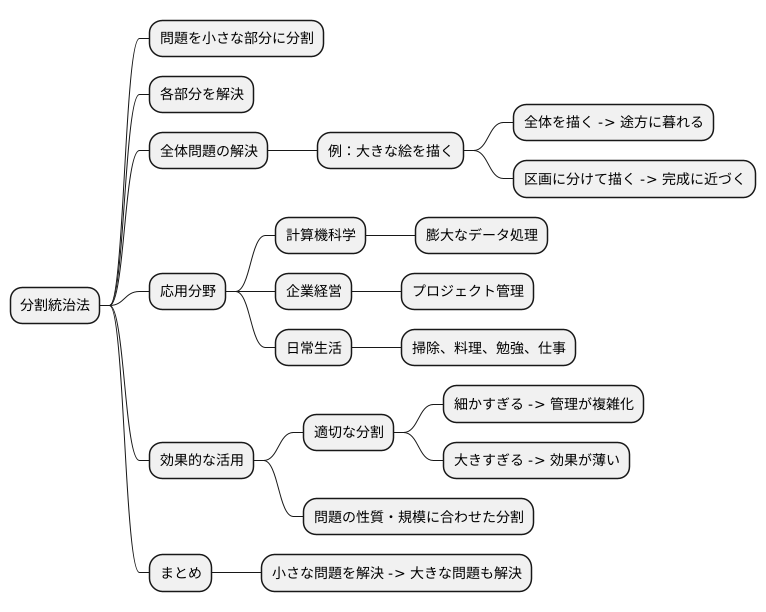
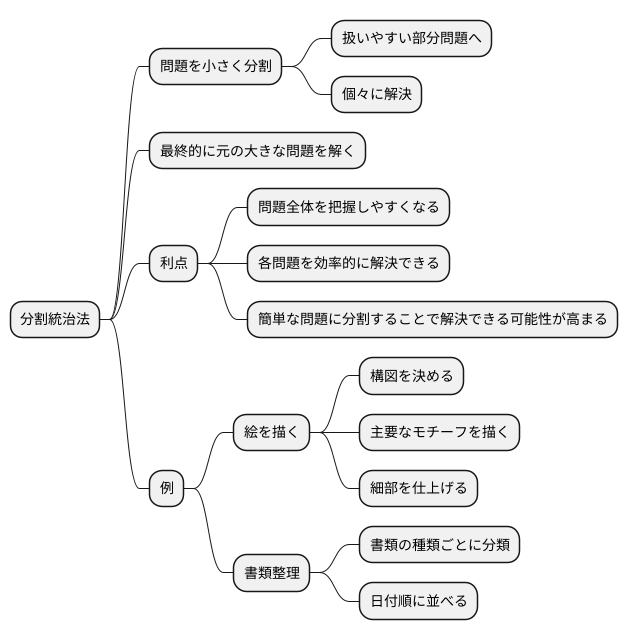
分割統治法とは、複雑で規模の大きな問題を、小さく扱いやすい部分問題に分解し、個々に解決していくことで、最終的に元の大きな問題を解く、効率的な問題解決の方法です。
例えるなら、大きな一枚の絵を描く時、いきなり全体を描き始めるのではなく、まず構図を決め、次に主要なモチーフを描き、最後に細部を仕上げていくように、段階的に作業を進めます。分割統治法もこれと同じように、大きな問題を小さな問題に分割することで、全体像を把握しやすくし、各々の小さな問題を効率的に解決できるようにします。
この方法は、一見すると複雑で解決が難しい問題でも、適切に分割することで、各部分問題は容易に解決できる可能性が高まるという利点があります。小さな問題を一つずつ解決していくことで、最終的には大きな問題全体の解決へと繋がっていくのです。
例えば、たくさんの書類を整理する必要があるとします。そのままではどこから手を付けて良いか分からず、途方に暮れてしまうかもしれません。しかし、書類の種類ごとに分類し、さらに日付順に並べるといった小さな作業に分割することで、整理がしやすくなります。一つ一つの作業は簡単なので、効率的に進めることができ、最終的には全ての書類を整理することができます。
このように、分割統治法は、問題解決の糸口を見つけにくい時や、大きな問題に圧倒されてしまいそうな時に効果的な手法と言えるでしょう。全体を把握し、適切に分割することで、まるで複雑な組み合わせ絵を解くように、一つずつピースを組み合わせて、完成させることができるのです。
適用範囲の広さ

分割統治法は、その名が示す通り、問題を小さな部分に分割し、それぞれを解決した後に、それらを組み合わせて全体の解決策を得る方法です。この方法は、様々な分野で驚くほど幅広く活用されています。
例えば、情報処理の分野では、膨大なデータを効率的に扱うために、分割統治法が欠かせません。大量のデータを整理する際に用いられる、高速な並べ替え処理を実現する手法(クイックソートやマージソートなど)は、まさに分割統治法に基づいています。これらの手法は、データを小さな塊に分割し、それぞれの塊を並べ替えた後、それらを再び組み合わせて全体を整理することで、処理速度を飛躍的に向上させています。
また、企業活動の場においても、分割統治法は重要な役割を果たしています。複雑で大規模な事業計画を扱う場合、計画全体を細かい作業単位に分割し、各担当者がそれぞれの作業に集中することで、効率的な管理を実現できます。それぞれの作業単位の成果を統合することで、全体としての一貫性と効率性を確保できるのです。これは、各部署やチームが独立して業務を進めながらも、最終的には組織全体の目標達成に貢献できるという点で、非常に効果的な手法と言えるでしょう。
さらに、日常生活においても、知らず知らずのうちに分割統治法を活用している場面は多くあります。例えば、大きな目標を達成するために、目標を小さな段階に分割し、一つずつ達成していくという方法は、まさに分割統治法の考え方です。資格試験の勉強や、長期的な貯蓄計画なども、この考え方に基づいて行うことで、成功の可能性を高めることができます。このように、分割統治法は、複雑な問題を解決するための強力な道具として、様々な場面で応用されているのです。
| 分野 | 例 | 説明 |
|---|---|---|
| 情報処理 | クイックソート、マージソート | 大量のデータを小さな塊に分割し、それぞれを並べ替えた後、再結合することで高速な並べ替えを実現。 |
| 企業活動 | 大規模な事業計画 | 計画を細かい作業単位に分割し、各担当者がそれぞれの作業に集中することで効率的な管理を実現。 |
| 日常生活 | 資格試験の勉強、長期的な貯蓄計画 | 大きな目標を小さな段階に分割し、一つずつ達成していく。 |
分割統治法の利点

分割統治法は、複雑な問題を効率的に解決するための優れた手法です。その利点は多岐に渡りますが、最も重要な点は問題の単純化と言えるでしょう。大きな問題をそのまま扱うのは困難ですが、分割統治法を用いることで、問題を小さな部分問題に分割できます。ちょうど、大きな一枚の絵を理解するために、まず細かな部分に分割して観察するようなものです。一つ一つの部分は理解しやすく、解決策も見つけやすいため、全体像の把握も容易になります。
分割統治法のもう一つの利点は並列処理が可能になることです。分割された部分問題はそれぞれ独立しているため、同時に処理を進めることができます。複数の作業員が同時に異なる部品を組み立て、最終的に一つの製品を完成させる工程を想像してみてください。各作業員は他の作業員を待つことなく、自分の作業に集中できます。これにより、全体の作業時間を大幅に短縮することが可能です。計算機の世界でも同様に、複数の処理装置を使って部分問題を同時に計算することで、処理速度を格段に向上させることができます。
さらに、分割統治法はプログラムを簡潔に記述できるという利点も持ちます。分割統治法は同じ処理を繰り返し行うという構造を持つため、再帰的な記述方法を用いることが可能です。これは複雑な処理を簡潔なコードで表現できることを意味し、プログラムの可読性や保守性を向上させる効果があります。複雑に入り組んだ指示書よりも、単純な指示を繰り返す方が理解しやすいのと同じです。このように、分割統治法は効率的な問題解決を実現するだけでなく、プログラムの開発効率向上にも貢献する強力な手法と言えるでしょう。
| 利点 | 説明 | 例え |
|---|---|---|
| 問題の単純化 | 大きな問題を小さな部分問題に分割し、個々に解決することで全体像の把握を容易にする。 | 大きな絵を細かな部分に分割して観察する。 |
| 並列処理の実現 | 分割された部分問題は独立しているため、同時に処理を進めることができ、全体の処理時間を短縮する。 | 複数の作業員が同時に異なる部品を組み立て、最終的に一つの製品を完成させる。 |
| プログラムの簡潔化 | 同じ処理を繰り返し行う構造を持つため、再帰的な記述方法を用いることができ、可読性や保守性を向上させる。 | 複雑に入り組んだ指示書よりも、単純な指示を繰り返す方が理解しやすい。 |
分割統治法の具体例

分割統治法は、複雑な問題を小さな部分に分割し、各部分を解決した後に全体を統合することで、効率的に解決策を見つける方法です。この手法は、様々な分野で応用されています。具体的な例をいくつか見てみましょう。
まず、地図上で最も短い道筋を見つけるという問題を考えてみます。目的地まで一度に道筋を計算しようとすると、非常に複雑で時間がかかります。しかし、分割統治法を使うと、この問題を簡単に解決できます。まず、地図全体をいくつかの区域に分割します。次に、各区域内での最も短い道筋を見つけます。そして最後に、区域と区域をつなぐ最も短い道筋を繋ぎ合わせることで、目的地までの全体の最短経路を求めることができます。このように、複雑な計算を小さな区域ごとの計算に分割することで、処理を効率化できます。
次に、たくさんの情報を整理するという問題を考えてみます。例えば、たくさんの商品の情報を整理する場合、全ての情報を一度に整理しようとすると、非常に時間がかかります。しかし、分割統治法を用いると、効率的に整理できます。まず、商品を種類ごとにグループ分けします。例えば、食品、衣料品、家電製品といった具合です。次に、各グループ内で商品をさらに細かく分類します。食品であれば、肉、魚、野菜などです。このように、情報を小さなグループに分割し、各グループ内で整理した後、グループ全体をまとめることで、全体を効率的に整理できます。
他にも、コンピュータの世界では、大きなデータを扱う際に分割統治法がよく使われます。例えば、大量の数字を順番に並べ替える「整列」という処理があります。この処理にも分割統治法が用いられます。まず、データをいくつかの小さなグループに分割します。次に、各グループ内でデータを順番に並べ替えます。最後に、並べ替えたグループを順番に統合することで、全体のデータを効率よく順番に並べ替えることができます。
このように、分割統治法は、様々な問題を解決するための強力な手法であり、日常生活からコンピュータの世界まで幅広く応用されています。
| 問題 | 分割方法 | 部分問題の解決 | 統合方法 |
|---|---|---|---|
| 地図上で最短経路を見つける | 地図を区域に分割 | 各区域内での最短経路を見つける | 区域間の最短経路を繋ぎ合わせる |
| たくさんの情報を整理する | 商品を種類ごとにグループ分け(食品、衣料品など) | 各グループ内で商品を細かく分類(肉、魚、野菜など) | 整理されたグループをまとめる |
| 大量の数字を順番に並べ替える(整列) | データを小さなグループに分割 | 各グループ内でデータを順番に並べ替える | 並べ替えたグループを順番に統合 |
分割の重要性

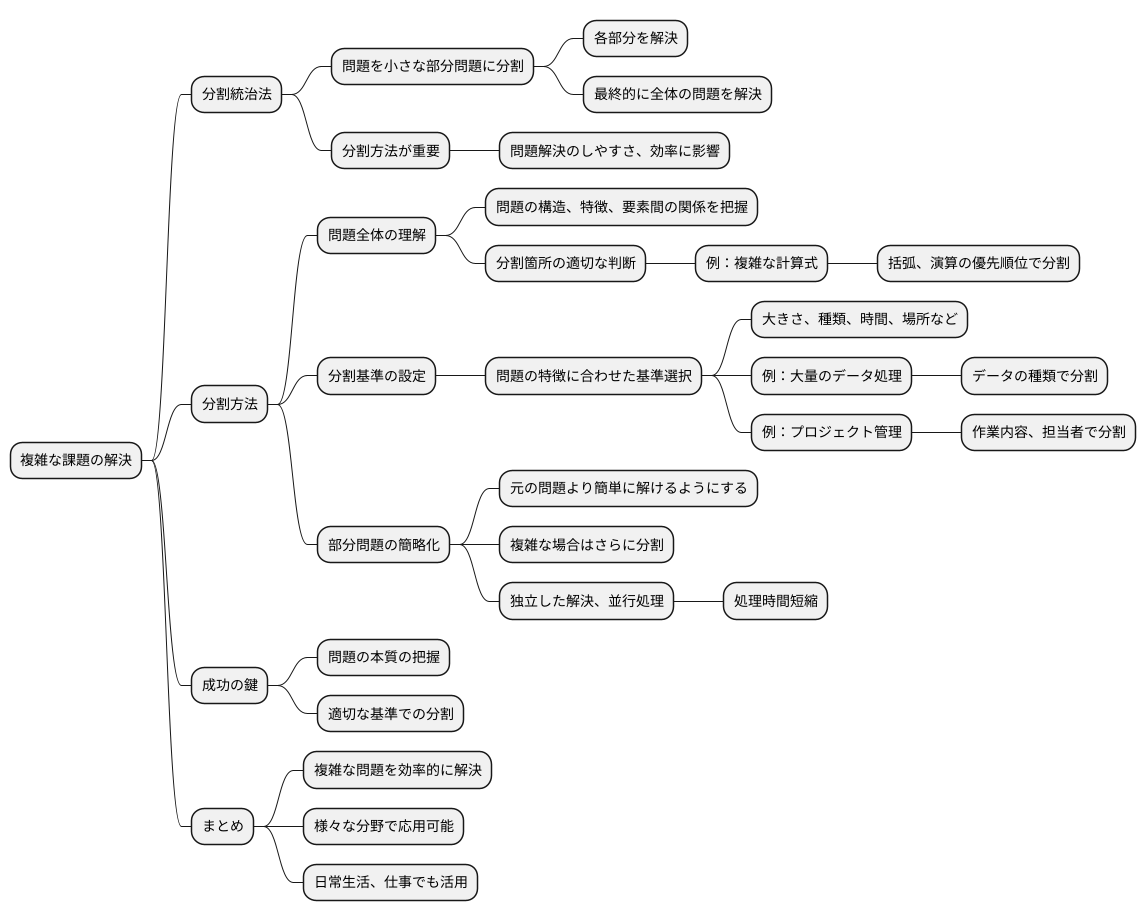
複雑な課題を解決するには、分割して考えることが大切です。分割統治法は、まさにこの考えに基づいた強力な解決手法です。大きな問題を小さな部分問題に分割し、それぞれを解決することで、最終的に全体の問題を解くことができます。しかし、この手法を効果的に使うには、分割方法が重要です。どのように分割するかによって、問題解決のしやすさや効率が大きく変わってきます。
まず、問題全体をしっかりと理解する必要があります。問題の構造や特徴、各要素間の関係などを把握することで、どこでどのように分割するのが適切かを判断できます。例えば、複雑な計算式を解く場合、括弧の中身や演算の優先順位などを考慮して分割することで、計算ミスを減らし、効率的に解くことができます。
分割の基準を適切に設定することも大切です。問題の特徴に応じて、大きさ、種類、時間、場所など、様々な基準で分割できます。例えば、大量のデータを処理する場合、データの種類ごとに分割することで、それぞれのデータに適した処理方法を適用できます。また、プロジェクトを管理する場合、作業内容や担当者ごとに分割することで、進捗状況を把握しやすくなり、効率的な管理につながります。
分割された各部分問題は、元の全体問題よりも簡単に解けるようにする必要があります。もし部分問題が依然として複雑であれば、さらに分割することを検討します。適切に分割することで、各部分問題は独立して解決できるようになり、並行処理が可能になる場合もあります。これにより、全体の処理時間を大幅に短縮できます。
分割統治法を成功させる鍵は、問題の本質を捉え、適切な基準で分割することです。分割方法を工夫することで、複雑な問題も効率的に解決できるようになります。分割統治法は、様々な分野で応用できる強力な手法です。日常生活でも、仕事でも、複雑な問題に直面した時は、分割して考えることを意識してみてください。
まとめ

私たちは日常生活の中で、大小様々な問題に直面します。難しい問題にぶつかった時、解決の糸口を見つける有効な方法の一つが、分割統治法です。分割統治法とは、複雑な問題を小さな部分に分割し、それぞれの部分を解決していくことで、最終的に全体の問題を解決する方法です。
例えるなら、大きな一枚の絵を描くことを想像してみてください。いきなり全体を描き始めると、どこから手を付けていいのか分からず、途方に暮れてしまうかもしれません。しかし、絵をいくつかの区画に分け、一つずつ丁寧に描いていくと、全体像を捉えながら、着実に完成に近づけることができます。これが分割統治法の基本的な考え方です。
分割統治法は、様々な分野で応用されています。例えば、計算機科学の分野では、膨大なデータを効率的に処理するために、分割統治法に基づいたアルゴリズムが用いられています。また、企業経営においても、複雑なプロジェクトを管理するために、プロジェクトを小さなタスクに分割し、それぞれのタスクの責任者を明確にすることで、効率的な運営を実現しています。日常生活でも、掃除や料理などの家事、あるいは勉強や仕事の計画など、様々な場面で分割統治法を活用することができます。
分割統治法を効果的に活用するためには、問題を適切に分割することが重要です。分割が細かすぎると、かえって管理が複雑になり、全体像を見失ってしまう可能性があります。反対に、分割が大きすぎると、個々の問題が依然として複雑なまま残ってしまうため、分割の効果が薄れてしまいます。問題の性質や規模に応じて、適切な分割方法を見極める必要があるでしょう。
小さな問題を一つずつ解決していくことで、最終的には大きな問題をも解決できることを、分割統治法は教えてくれます。目の前の困難に圧倒されそうになった時は、分割統治法を思い出してみてください。きっと、解決への道筋が見えてくるはずです。