ベイズ統計学入門

AIを知りたい
先生、「ベイズ統計学」って難しそうでよくわからないです。簡単に説明してもらえますか?

AIエンジニア
そうだね、確かに少し難しいかもしれないね。簡単に言うと、ベイズ統計学は、最初に「たぶんこれくらいの確率で起こるだろう」と予想を立てて、その後、新しい情報が入ってくるたびに、その予想を修正していく考え方だよ。例えば、明日の天気予報で、最初は雨が降る確率を30%と予想していたとする。でも、夕方になって雲行きが怪しくなってきたら、雨が降る確率を60%に修正する、これがベイズ統計学の考え方だよ。

AIを知りたい
なるほど。最初に予想を立てて、それを修正していくんですね。でも、最初の予想ってどうやって立てるんですか?

AIエンジニア
良い質問だね。最初の予想は、これまでの経験や知識をもとに決めるんだ。明日の天気の例でいうと、過去の気象データや、天気予報士の経験に基づいて、最初の30%という確率が決まっているんだよ。そして、新しい情報、例えば雲行きが怪しくなった、という情報が入ってきたら、その情報を元に確率を修正していくんだ。
ベイズ統計学とは。
人工知能に関係する言葉である「ベイズ統計学」について説明します。ベイズ統計学は、見本がなくても、データが足りなくても、なんとか確率を導き出す方法です。確率には、実際に起こる確率と、個人が思う確率の二種類があります。ベイズ統計学は、個人が思う確率を扱う統計学です。どのように計算するかというと、まず「あることが起こる確率」を最初に決めます(これを「事前の確率」と言います)。そして、新しい情報が手に入るたびに「あることが起こる確率」(これを「事後の確率」と言います)を新しくしていきます。そうやって、本当に起こりそうな確率(個人が思う確率)を導き出すのです。「事前の確率」とは、「データを見る前に考えていた確率」のことですが、データが全くないという意味ではありません。「事前の確率」と「事後の確率」は、あくまでも新しくデータが手に入る前後の確率です。手に入れたデータを使って確率を新しくしていくことを「ベイズ更新」と言います。
不確実性への対応

私たちの暮らす世界は、予測できない出来事に満ちています。明日の天気予報が外れることもありますし、経済の動向や新しい商品の売れ行きも、確実に言い当てることは難しいものです。このような予測のつかない状況に立ち向かうための強力な道具として、ベイズ統計学があります。ベイズ統計学は、物事がどれくらい確からしいかを確率を使って表し、不確かな事象について推論を行います。
ベイズ統計学の特徴は、過去の経験や知識を確率という形で取り入れることができる点にあります。例えば、過去の天気予報の的中率や、似たような商品の売れ行きといった情報を確率で表し、これらを事前情報として利用します。そして、新しい情報が入ってくるたびに、この事前情報と新しい情報を組み合わせ、より確かな予測へと更新していきます。天気予報で言えば、朝方に雲行きが怪しくなってきたという新たな情報を得れば、雨の確率を高く修正するといった具合です。
従来の統計学では、十分な量のデータが集まらないと、分析が難しいという問題がありました。しかし、ベイズ統計学では、限られたデータでも分析を行うことができます。これは、少ないデータしかない場合でも、過去の経験や専門家の知識といった事前情報を活用できるためです。例えば、新しい薬の効果を調べるための試験では、参加者を多く集めるのが難しい場合があります。ベイズ統計学を使えば、少ない参加者から得られたデータと、過去の類似の薬の効果に関する情報を組み合わせ、新薬の効果や副作用の可能性について確率的な評価を行うことができます。このように、ベイズ統計学は、情報が不足している状況でも、意思決定を助けるための判断材料を提供してくれるのです。
| ベイズ統計学 | 説明 | 例 |
|---|---|---|
| 特徴 | 過去の経験や知識を確率という形で取り入れ、不確かな事象について推論を行う。新しい情報が入るたびに、事前情報と新しい情報を組み合わせ、より確かな予測へと更新していく。 | 過去の天気予報の的中率や類似商品の売れ行きを事前情報として利用し、朝方に雲行きが怪しくなってきたという新たな情報で雨の確率を高く修正する。 |
| 利点 | 限られたデータでも分析を行うことができる。情報が不足している状況でも、意思決定を助けるための判断材料を提供する。 | 新薬の効果を調べる試験で、少ない参加者から得られたデータと過去の類似の薬の効果に関する情報を組み合わせ、新薬の効果や副作用の可能性について確率的な評価を行う。 |
主観確率という考え方

物事の起こりやすさを数値で表すとき、私たちはよく確率という言葉を使います。たとえば、サイコロを振って1が出る確率は六分の一、といった具合です。これは、起こりうるすべての場合が均等に現れるという前提に基づいた考え方で、客観的な確率と言えます。しかし、現実の世界では、このようにすべての場合が均等に現れるとは限りません。明日の天気のように、様々な要因が複雑に絡み合って結果が決まる場合も少なくありません。このような状況で、物事の起こりやすさをどのように評価すればよいのでしょうか。そこで登場するのが、主観確率という考え方です。
主観確率とは、文字通り、個人が主観的に物事の起こりやすさを評価したものです。たとえば、「明日は雨が降るだろう」と感じる度合いを確率で表すことができます。過去の天気や天気予報などをもとに、「明日は70%の確率で雨が降る」と考えるのも、主観確率の一例です。もちろん、人によって経験や知識は異なるため、同じ事象に対しても主観確率は異なることがあります。ある人は明日の降水確率を70%と考える一方で、別の人は80%と考えるかもしれません。これは、主観確率が個人の信念を反映しているからです。
この主観確率という考え方は、ベイズ統計学という学問において中心的な役割を果たします。ベイズ統計学では、まず最初に、事前確率と呼ばれる初期値を設定します。これは、データを得る前の段階での主観的な確率です。そして、新しい情報やデータが得られるたびに、この事前確率を更新していきます。更新された確率は、事後確率と呼ばれます。このように、ベイズ統計学では、主観確率を更新しながら、より確かな予測に近づけていくのです。
従来の統計学では、データが十分にない場合、分析が難しいという問題がありました。しかし、ベイズ統計学では、主観確率を用いることで、データが不足している場合でも、過去の経験や専門家の知恵を活かして分析を行うことができます。これは、不確実性が高い状況での意思決定を可能にする大きな利点であり、ビジネスや医療など、様々な分野で応用されています。
| 確率の種類 | 定義 | 例 | 特徴 |
|---|---|---|---|
| 客観確率 | 起こりうるすべての場合が均等に現れるという前提に基づいた確率 | サイコロを振って1が出る確率 | 事象の発生頻度に基づく |
| 主観確率 | 個人が主観的に物事の起こりやすさを評価した確率 | 明日の降水確率を70%と考える | 個人の信念を反映、ベイズ統計学で利用 |
| ベイズ統計学 | 説明 |
|---|---|
| 事前確率 | データを得る前の段階での主観的な確率 |
| 事後確率 | 新しい情報やデータによって更新された確率 |
| 特徴 | 主観確率を更新、データ不足時にも過去の経験や専門家の知恵を活用可能 |
ベイズ更新:予測の進化

私たちは常に未来を予測しようとしています。明日の天気、来月の売上、人生の様々な場面で予測は欠かせません。ベイズ更新は、そうした予測をより確かなものにするための強力な手法です。ベイズ更新とは、最初に持っている知識や経験を基に予測を行い、新しい情報が入ってくるたびに、その予測を修正していく方法です。まるで、粘土をこねるように、少しずつ形を変えながら、より現実に近い像を作り上げていくようなものです。
例として、商品の売れ行き予測を考えてみましょう。新しい商品を発売する際、最初の予測は過去の類似商品のデータや市場調査に基づいて行います。これが最初の予測、つまり「事前確率」です。商品を発売すると、実際の売上のデータが入ってきます。この新しい情報が「観測データ」です。ベイズ更新では、この観測データを使って、最初の予測を修正し、より正確な予測(「事後確率」)を導き出します。最初の予測が外れていたとしても、実際のデータを取り入れることで、予測を現実に近づけることができるのです。
この事後確率は、次の予測の事前確率として使われます。つまり、ベイズ更新は一度きりのものではなく、継続的に行われるのです。例えば、商品の売上に影響を与える広告キャンペーンを実施したとします。キャンペーンの効果に関するデータも新たな観測データとして取り込み、再び予測を更新します。このように、ベイズ更新は、끊임없이新しい情報を学び、予測の精度を高めていくことができるのです。まるで、経験を積むことで、より的確な判断ができるようになる人間の学習プロセスと似ています。だからこそ、ベイズ更新は、天気予報、医療診断、金融市場の予測など、様々な分野で活用され、未来への展望をより鮮明なものにしているのです。
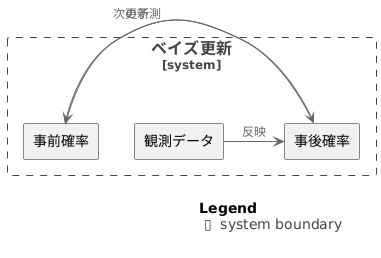
事前確率と事後確率

物事の起こる可能性を数値で表すことを確率と言いますが、統計学の一分野であるベイズ統計学においては、事前確率と事後確率という二つの大切な考え方が出てきます。これらは、まるで表裏一体の関係にあると言えるでしょう。
まず、事前確率とは、文字通り、実際にデータを集める前に設定する確率のことです。これは、過去の経験や既に知っている知識、あるいは主観的な考えに基づいて決めます。例えば、明日の天気予報が雨だと聞いたとします。そこで、傘を持って出かけるかどうかを考えます。過去の経験から、天気予報が雨でも実際には晴れることが何度かあったことを思い出したとしましょう。すると、「明日の天気予報は雨だが、実際には晴れる確率は30%くらいだろう」と考えるかもしれません。この30%という数値が、事前確率に当たります。
次に、事後確率について説明します。これは、実際にデータを観測した後で、事前確率を修正した確率のことです。例えば、朝起きて窓の外を見ると、空はどんよりと曇っており、雨が降りそうな気配です。この新たな情報を得たことで、「やっぱり明日の天気予報は雨のようだから、実際にも雨が降る確率は80%くらいに上がった」と考えるかもしれません。この80%という数値が、事後確率です。つまり、事後確率は、新たな情報によって更新された、より確かな確率と言えるでしょう。
ベイズ統計学の重要な点は、この事後確率が、次の分析における事前確率として使われるというところにあります。つまり、明日の朝、雨が降っていたとしましょう。この場合、次の日の天気予報を考える際に、今回得られた「実際には雨が降った」という情報は、次の事前確率を決める上で重要な要素となります。このように、ベイズ統計学は、データを得るたびに学び、予測の正確さを高めていくという手順を繰り返します。そして、データが集まるほど、予測の確かさは上がっていくと考えられます。
| 概念 | 説明 | 例 |
|---|---|---|
| 事前確率 | データを集める前に、過去の経験や知識に基づいて設定する確率 | 天気予報が雨でも、実際には晴れる確率は30% |
| 事後確率 | 実際にデータを観測した後で、事前確率を修正した確率 | 朝、空が曇っているのを見て、雨が降る確率は80%に上がった |
応用範囲の広がり

ベイズ統計学は、様々な分野で応用され、私たちの生活にも深く関わっています。その応用範囲の広がりについて、具体的に見ていきましょう。
まず、医療の分野では、ベイズ統計学は病気の診断や治療方針の決定を支援する重要な役割を担っています。ある症状が現れたときに、それがどの病気に由来するのかを確率的に判断する際に、ベイズ統計学が役立ちます。過去の症例データや検査結果などをもとに、患者さんの症状から考えられる病気の可能性を計算し、最も可能性の高い病気を特定することで、迅速な診断と適切な治療方針の決定をサポートします。
経済学の分野では、経済の動きを予測したり、金融リスクを管理したりする際にベイズ統計学が活用されています。過去の経済指標や市場の動向といった大量のデータに基づいて、将来の経済状況や市場の変動を予測することができます。また、投資におけるリスク評価やポートフォリオの最適化など、金融商品の開発やリスク管理にも役立っています。
情報工学の分野では、人工知能や機械学習の基盤技術としてベイズ統計学が応用されています。迷惑メールの自動振り分けや、自動運転技術における周囲の状況判断など、身近な技術にもベイズ統計学が活用されています。大量のデータからパターンや規則性を学習し、将来の予測や判断を行う機械学習アルゴリズムの多くは、ベイズ統計学の考え方に基づいて開発されています。
このように、ベイズ統計学は不確実性が高い状況下での意思決定を支援する強力な手法として、幅広い分野で役立っています。今後、データの重要性がますます高まるにつれて、ベイズ統計学の重要性はさらに増していくでしょう。
| 分野 | 応用例 |
|---|---|
| 医療 | 病気の診断、治療方針の決定 |
| 経済学 | 経済予測、金融リスク管理、投資リスク評価、ポートフォリオ最適化 |
| 情報工学 | 人工知能、機械学習(迷惑メール振り分け、自動運転) |
より良い意思決定のために

確かな事など何もないこの世界で、私たちは日々大小さまざまな決定を迫られています。朝ごはんに何を食べるかという些細な事から、人生を左右する大きな決断まで、その内容は多岐に渡ります。このような不確かな状況で、より良い選択をするための強力な道具となるのが、ベイズ統計学です。
ベイズ統計学は、過去の経験や知識を確率という形で表現します。例えば、過去のデータから「明日雨が降る確率は70%」といった予測を立てることができます。そして、新たな情報が入ってくるたびに、この確率を更新していくのです。例えば、天気予報で「明日は晴れ」と報じられたら、雨が降る確率は下方修正されます。このように、常に最新の情報を加味することで、より精度の高い予測を立てることができるのです。
ベイズ統計学の大きな強みは、データが十分にない場合でも、専門家の知見や過去の経験を活かせるという点です。新しい製品の売れ行き予測など、データが不足しがちな状況でも、過去の類似製品の販売実績や市場の動向といった情報を取り入れることで、ある程度の予測を行うことができます。
ベイズ統計学は、すでに様々な分野で活用されています。企業では、新製品の開発や市場分析、顧客行動の予測などに役立てられています。医療の現場では、患者の症状や検査結果から病気を診断する際に、ベイズ統計学に基づいた手法が用いられています。また、政策決定の場面でも、政策の効果予測やリスク評価などに活用されています。
情報があふれ、変化の激しい現代社会において、ベイズ統計学はますます重要な役割を担っていくでしょう。複雑な状況を適切に理解し、より良い決定を下すために、ベイズ統計学は、私たちにとって無くてはならない道具となるはずです。
| ベイズ統計学とは | 内容 |
|---|---|
| 定義 | 過去の経験や知識を確率で表現し、新たな情報で確率を更新することで、より精度の高い予測を行う統計学。 |
| 利点 | データが不十分でも、専門家の知見や過去の経験を活用できる。常に最新情報を取り入れ、予測精度を高める。 |
| 活用例 |
|
| 将来性 | 情報化社会、変化の激しい現代において重要な役割を担う。複雑な状況理解、意思決定に不可欠な道具。 |
